Rugs in a Room
Inside a room of area 5 m 2 , you place 9 rugs, each of area 1 m 2 having an arbitrary shape.
If the least overlap area ( in m 2 ) of two rugs in this room can be expressed as B A , where A and B are coprime positive integers, find A + B .
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
we will focus on numbers (areas), and ignore the shapes, since they can be arbitrary.
this is the sequence of my thought process:
-
Assumption : the minimizing layout will not involve 3 overlapping rugs. (this start with pure intuition, proven later)
-
Layout : assuming a ring shaped room, the layout is shown below.

-
Find the overlapping area y. room area = 9 x + 9 y rug area = 2 x + y ∴ x = 9 4 , y = 9 1 ∴ a + b = 1 + 9 = 1 0 = 5 = 1
-
Proving assumption in step 1.
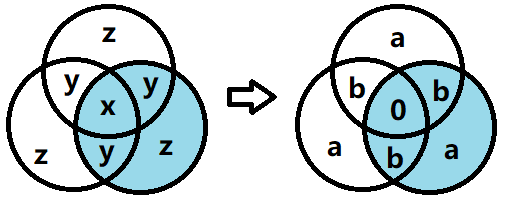 We will focus on 3 rugs. Making another assumption from intuition, minimizing layout will be symmetrical (left). It can be redistributed (right) such that (1) the total covered area remain unchanged, and (2) 3 overlapping area is 0.
covered area
=
x
+
3
y
+
3
z
rug area
=
x
+
2
y
+
z
∴
a
=
−
3
1
x
+
z
,
b
=
3
2
x
+
y
=
3
a
+
3
b
=
a
+
2
b
Hence, two rugs overlapping area decreases from
(
x
+
y
)
to
(
3
2
x
+
y
)
, (partially) proving the assumption.
We will focus on 3 rugs. Making another assumption from intuition, minimizing layout will be symmetrical (left). It can be redistributed (right) such that (1) the total covered area remain unchanged, and (2) 3 overlapping area is 0.
covered area
=
x
+
3
y
+
3
z
rug area
=
x
+
2
y
+
z
∴
a
=
−
3
1
x
+
z
,
b
=
3
2
x
+
y
=
3
a
+
3
b
=
a
+
2
b
Hence, two rugs overlapping area decreases from
(
x
+
y
)
to
(
3
2
x
+
y
)
, (partially) proving the assumption.
-
Loose ends :
(a) 4 overlapping rugs and above?
(b) Is there a minimizing layout which is not symmetrical?
(c) What if a = − 3 1 x + z < 0 in step 4?
The solution is by no means rigorous, but my patience is limited.
Consider a point Q , which is distributed uniformly at random in the room. Also, let us denote the event that the i th rug contains the point Q by E i . We have P ( E i ) = 5 1 , ∀ i = 1 , 2 , … , 9 . Now, using Bonferroni's Inequality , we have 1 ≥ P ( ∪ i = 1 9 E i ) ≥ i = 1 ∑ 9 P ( E i ) − 1 = i < j = 9 ∑ P ( E i ∩ E j ) ≥ 5 9 − ( 2 9 ) max P ( E i ∩ E j ) . This implies, max P ( E i ∩ E j ) ≥ 4 5 1 . Since the total area of the room is 5 m 2 , it follows that the least amount of overlap area of two rugs is at least 5 × 4 5 1 = 9 1 . Now, it is easy to come up with symmetrical rugs (see, e.g., the annular room layout in the other solution attempt) which meets this bound.
Note: This is a nice example of using Probabilistic (or more generally, Measure theoretic) ideas to solve a seemingly Geometrical problem.