Rule of sign

First calculate $\cos(A)$ and $\cos(B)$ using $\sin^2 \theta+\cos^2 \theta=1$

$\cos(A)=\sqrt{1-\left(\dfrac{4}{5}\right)^2}=\dfrac{3}{5} \\ \cos(B)=\sqrt{1-\left(\dfrac{12}{13}\right)^2}=\dfrac{5}{13}$

We only use the angles in the first quadrant to make sure that the triangle exists. Now:

$A+B+C=\pi \\ C=\pi-(A+B) \\ \sin(C)=\sin(\pi-(A+B)) \\ \sin(C)=\sin(A+B) \\ \sin(C)=\sin(A)\cos(B)+\sin(B)\cos(A) \\ \sin(C)=\dfrac{4}{5} \cdot \dfrac{5}{13}+\dfrac{12}{13} \cdot \dfrac{3}{5} \\ \sin(C)=\dfrac{20}{65}+\dfrac{36}{65}=\boxed{\dfrac{56}{65}}$

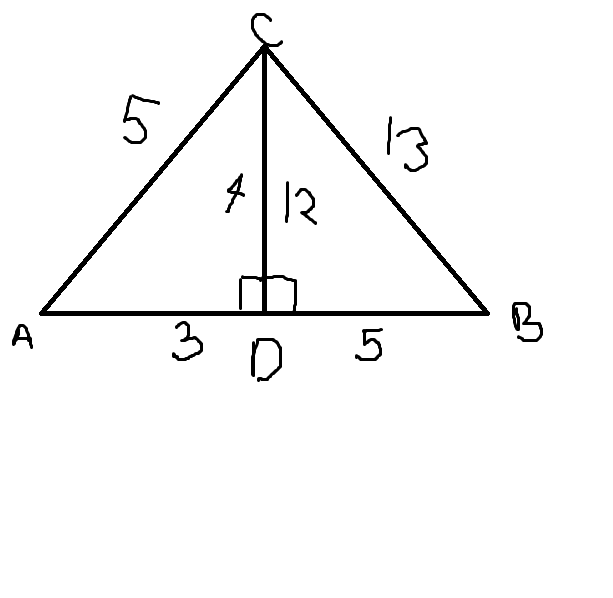
In the image, $CD$ is constructed so that $CD\perp AB$ .

$\sin(A)=\frac{CD}{AC}=\frac{4}{5}$

$\cos(A)=\frac{AD}{AC}=\frac{3}{5}$

$\sin(B)=\frac{CD}{BC}=\frac{12}{13}$

$\cos(B)=\frac{BD}{BC}=\frac{5}{13}$

$\sin(C) = \sin((90-A)+(90-B)) = \sin(180-(A+B)=\sin(A+B) = \sin(A)\cos(B)+\cos(A)\sin(B) = \frac{4}{5}\times\frac{5}{13}+\frac{3}{5}\times\frac{12}{13}=\boxed{\frac{56}{65}}$

sin b = 12/13 multiplying it by 5 then sin b = 60/65 sin a =4/5 multiplying it by 13 then sin a = 52/65 . so we can conclude from sin (theeta) = opposite/ hypotenuse , that 65 is hypotenuse . so the options may be B or C by taking a chance i chose the option 56/65 its correct PLEASE POST A BETTER SOLUTION

The problem can also be solved by equating the opposite sides (the altitude) of $\angle A$ and $\angle B$ see the diagram below.

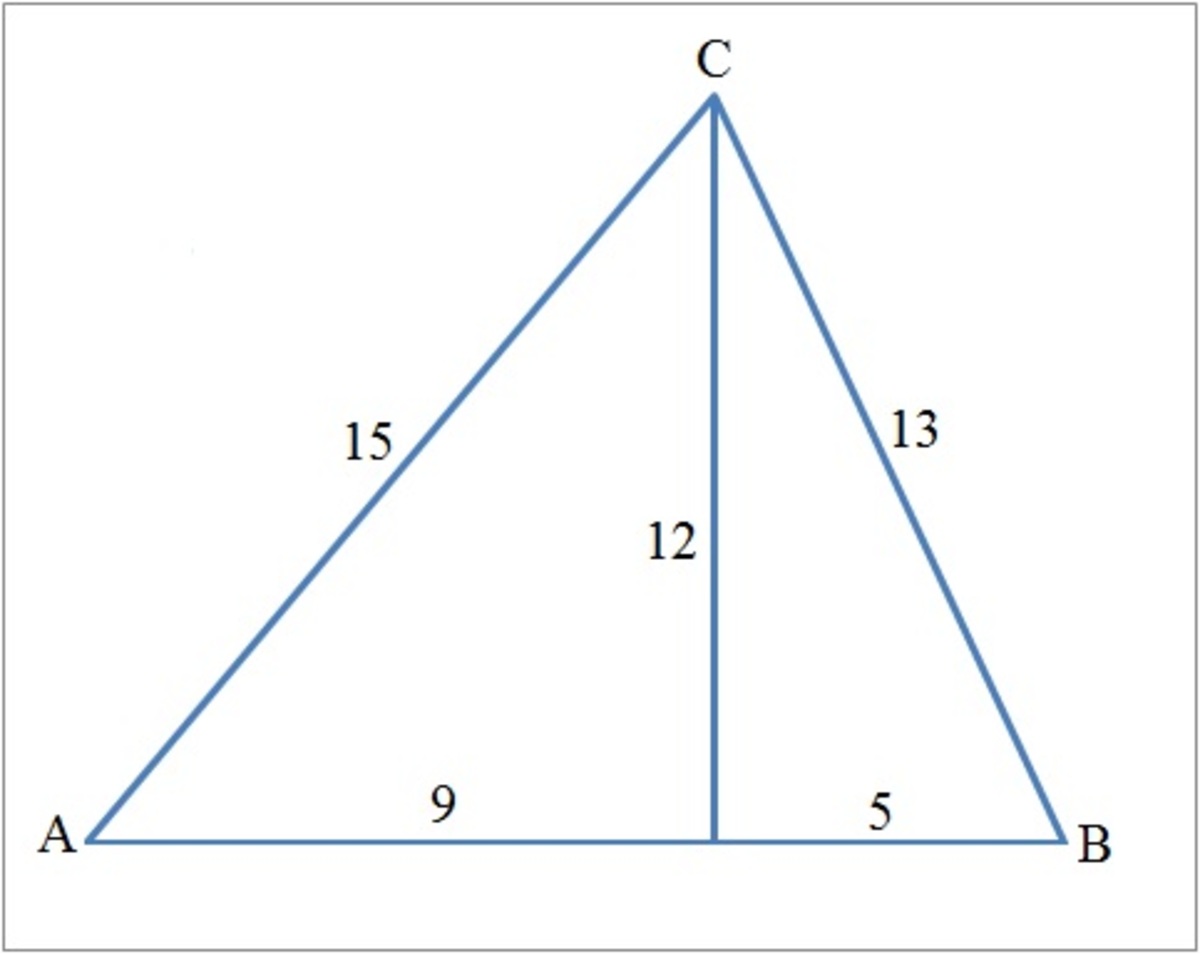
Then by using Cosine Rule, we have:

$\begin{aligned} 14^2 & = 15^2+13^2-2(15)(13)\cos{(C)} \\ \cos{(C)} & = \frac{15^2+13^2 - 14^2} {2(15)(13)} = \frac{33}{65} \\ \Rightarrow \sin{(C)} & = \sqrt{1-\left(\frac{33}{65}\right)^2} = \boxed{\dfrac{56}{65}} \end{aligned}$

ABC is a triangle so total 180 degree

so sin inverse(4/5)+sin inverse(12/13)=120.51

180-120.51=59.49

sin(59.49)=0.86154

which is 56/65