Running Between Cars

Calculus Level 3

Two cars, 270 miles apart, start driving toward each other. One car has a speed of 40mph and the other has a speed of 50mph. Chris stands at the midpoint between the two cars. He runs toward one of the cars, touches its hood, then runs towards the other car, touches its hood, and repeats this until the cars collide (and presumably bounce off of him). Chris travels at a speed of 60mph at all times.

Let $v(t)$ denote Chris’s velocity in mph and $t_0$ denote the amount of time that has elapsed at the moment the cars collide (and presumably bounce off of Chris). Evaluate:

$\left|\int_{0}^{t_0}v(t)dt\right| + \int_{0}^{t_0}\left|v(t)\right|dt$

The answer is 195.

2 solutions

Clara Blackstone
Oct 16, 2015

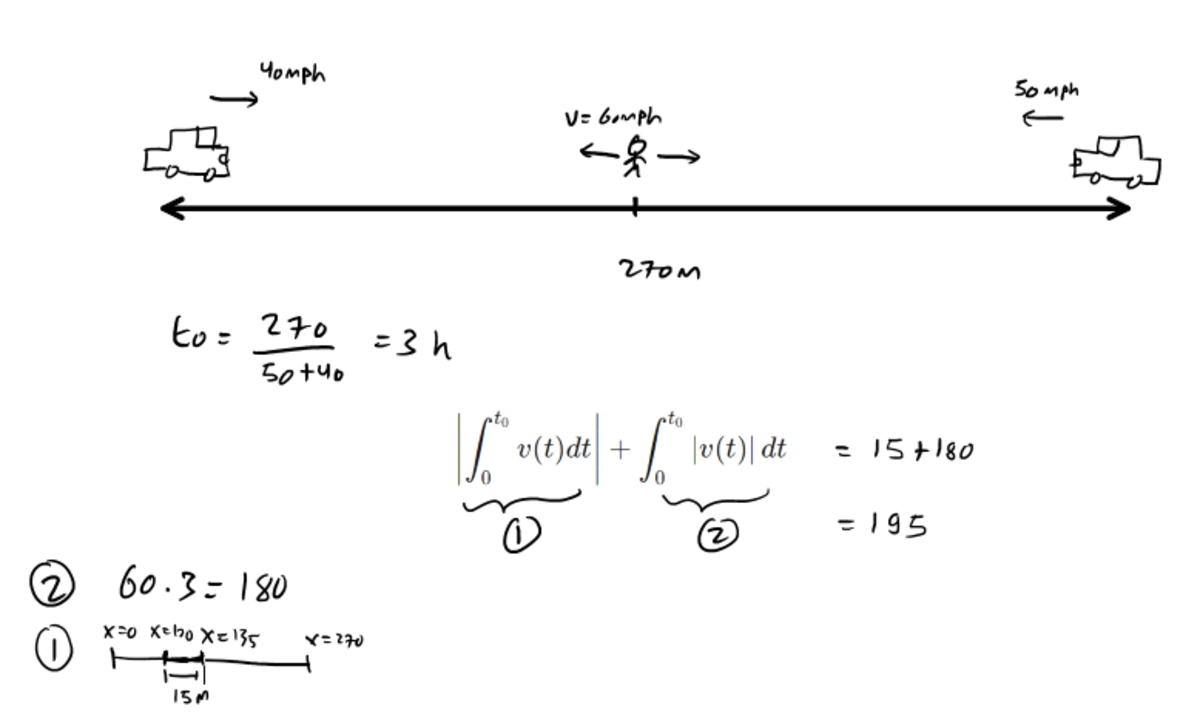
Because the cars have a collective speed of 90mph when driving toward each other, they will collide after $\dfrac{270 \text{ miles}}{90 \text{ mph}} = 3 \text{ hours}$ . Suppose that the slower car starts at $x = 0$ and moves rightward. Since it travels for 3 hours at 40 mph, then it will end at $x = 120$ .

The first integral represents the absolute value of Chris's displacement. Since Chris starts at a point 135 miles from the first car (or $x = 135$ ) and he ends at $x = 120$ , the absolute value of his displacement is 15miles.

The second integral represents the total distance traveled by Chris. Since he travels at 60mph for 3 hours, his total distance traveled is 180 miles.

Therefore $\left|\int_{0}^{t_0}v(t)dt\right| + \int_{0}^{t_0}\left|v(t)\right|dt = 15 + 180 = 195.\square$

Bostang Palaguna
Dec 28, 2020

Running Between Cars

The answer is 195.

2 solutions

0 pending reports