Running inside a Pythagorean Triangle

Geometry Level 3

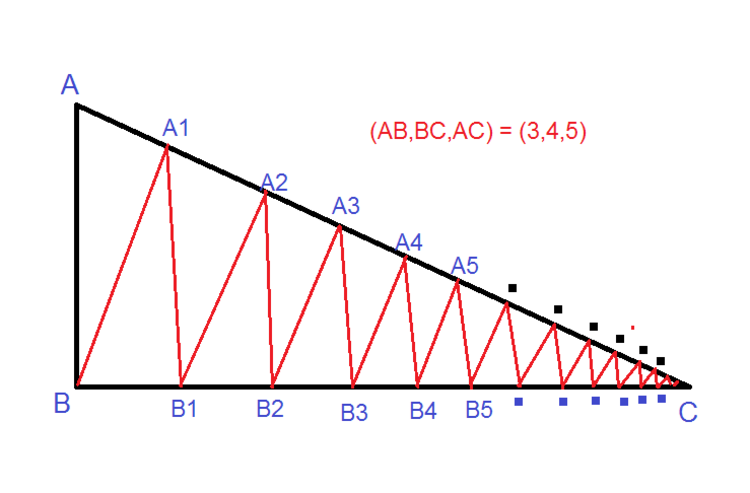Diagram above is not to scale.

Kevin went to a park for a refreshing run. The park had the shape and dimensions of the pythagorean triangle (3,4,5).

He ran from point B to point C by choosing the following path

B--A1--B1--A2--B2--A3--B3--A4--B4--------------C.

Points (A1, A2, A3,........) on AC are shortest distances from points (B, B1, B2,.....) on BC respectively

Similarly, Points (B1, B2, B3,........) on BC are shortest distances from points (A1, A2, A3,.....) on AC respectively

Assuming Kevin is a point. Find the total distance covered by Kevin by taking the above path running from B to C?

Source: Own Work


The answer is 12.

John Samuel by John Samuel , 40, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Finn Hulse
May 21, 2014

I simply realized this was an infinite series:

12 5 + 48 25 + ⋯ + 3 × 4 n 5 n \dfrac{12}{5}+\dfrac{48}{25}+ \dots+ \dfrac{3 \times 4^n}{5^n}

And evaluating the sum, the answer is 12 \boxed{12} . Sorry about the lack of depth/explanation. Great problem though @John Samuel ! :D

2 Helpful 0 Interesting 0 Brilliant 0 Confused

Yes, the series obtained is: 12 / 5 + 48 / 25 + . . . . . + 3 ( 4 n ) / 5 n 12/5+48/25+.....+{3(4^{n})/5^{n}} Therefore, answer is 12 \boxed{12}

Kïñshük Sïñgh - 6 years, 11 months ago

Log in to reply

please explain the series, how do you make this pattern?

Sanjoy Roy - 6 years, 4 months ago

Did the same thing!

Chris Hambacher - 7 years ago

Log in to reply

Cool. I'm still not quite sure why exactly it works but somehow it does. I just calculated the first few cases and then realized there was a pattern and generalized a formula. :D

Finn Hulse - 7 years ago
Bill Bell
Nov 6, 2014 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
 
from sympy import *

B = [ Point ( 0, 0 ) ]
AC = Line ( Point ( 0, 3 ), Point ( 4, 0 ) )

A = [ ]
hops = [ ]
for i in range ( 10 ) :
    A . append ( AC . intersection ( AC . perpendicular_line ( B [ -1 ] ) ) [ 0 ] )
    B . append ( Point ( A [ -1 ] . x, 0 ) )
    hops . append ( B [ -2 ] . distance ( A [ -1 ] ) + A [ -1] . distance ( B [ -1] ) )

a = hops [ 0 ]

for hop_a, hop_b in zip ( hops [ : -1], hops [ 1 : ]) :
    print hop_b / hop_a # to verify that it's a geometric series

r = hops [ 1 ] / hops [ 0 ]

print a, r, a / ( 1 - r )

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...