Running Track

Geometry Level 3

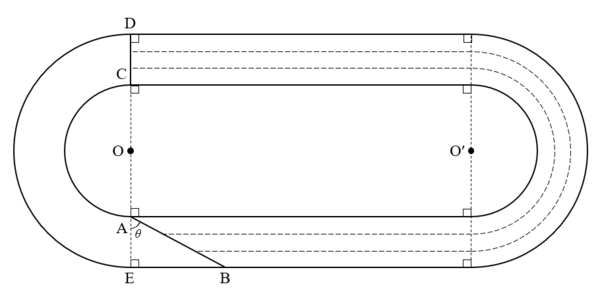
Runners run the track above from start line A B \mathrm{AB} to end line C D \mathrm{CD} . The curve part of the track is a half circle which shares O , O ′ \mathrm{O, O^\prime} as the center. What is the value of θ \theta to the nearest degree?. (All runners should run equal distances)


The answer is 72.

Junghwan Han by Junghwan Han , 19, South Korea

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Chew-Seong Cheong
Jan 22, 2019

Let the external radius of the circular part of the track O E = R OE=R and the internal radius O A = r OA=r . To be a fair track, we have:

A C = B D 2 O O ′ + π r = 2 O O ′ − E B + π R π r = − E B + π R = − A E tan ⁡ θ + π R = − ( R − r ) tan ⁡ θ + π R ⟹ ( R − r ) tan ⁡ θ = π ( R − r ) tan ⁡ θ = π ⟹ θ ≈ 72 ∘ \begin{aligned} AC & = BD \\ 2OO'+\pi r & = 2OO' - EB + \pi R \\ \pi r & = - EB + \pi R \\ & = - AE \tan \theta + \pi R \\ & = - (R-r) \tan \theta + \pi R \\ \implies (R-r) \tan \theta & = \pi (R-r) \\ \tan \theta & = \pi \\ \implies \theta & \approx \boxed {72}^\circ \end{aligned}

3 Helpful 0 Interesting 0 Brilliant 0 Confused

Cool problem. Entering t a n − 1 π tan^{-1}\pi feels so wrong. It looks like the type of error students make when learning trigonometry -- confusing the angle with the tangent ratio. The dissonance compounds when we use π \pi which looks like an angle in radians but then we answer in degrees.

Jeremy Galvagni - 2 years, 4 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...