Russian Doll problem
This is problem 7 of AIME 1987.
The function f is defined on the integers, and satisfies.
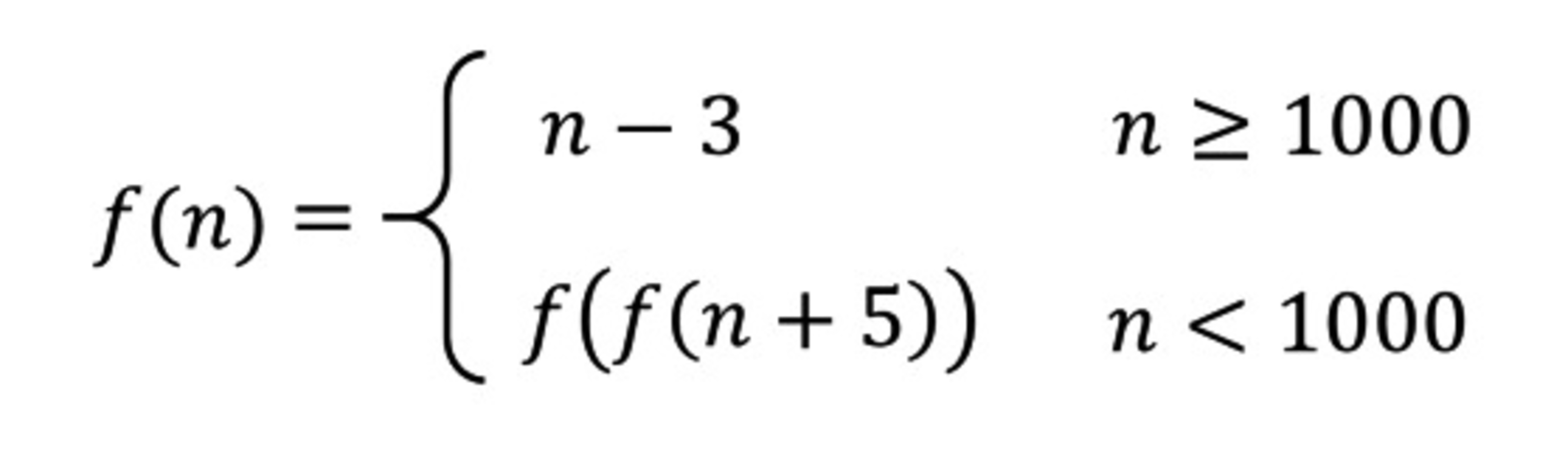
Find f(84).
The answer is 997.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The function f can be readily seen (by induction on n ) to be equal to f ( n ) = ⎩ ⎨ ⎧ n − 3 9 9 7 9 9 8 n ≥ 1 0 0 0 n ≤ 9 9 9 , n e v e n n ≤ 9 9 9 , n o d d and hence f ( 8 4 ) = 9 9 7 .
When you say "induction on n ", you mean to let n decrease from 1000, right?
Log in to reply
Yes. The inductive hypothesis is that the formula works for n ≥ k , and we use this to deduce the correctness of the formula for n = k − 1 . The "ground step" n = 1 0 0 0 is trivial.
 Solution using Python
Solution using Python
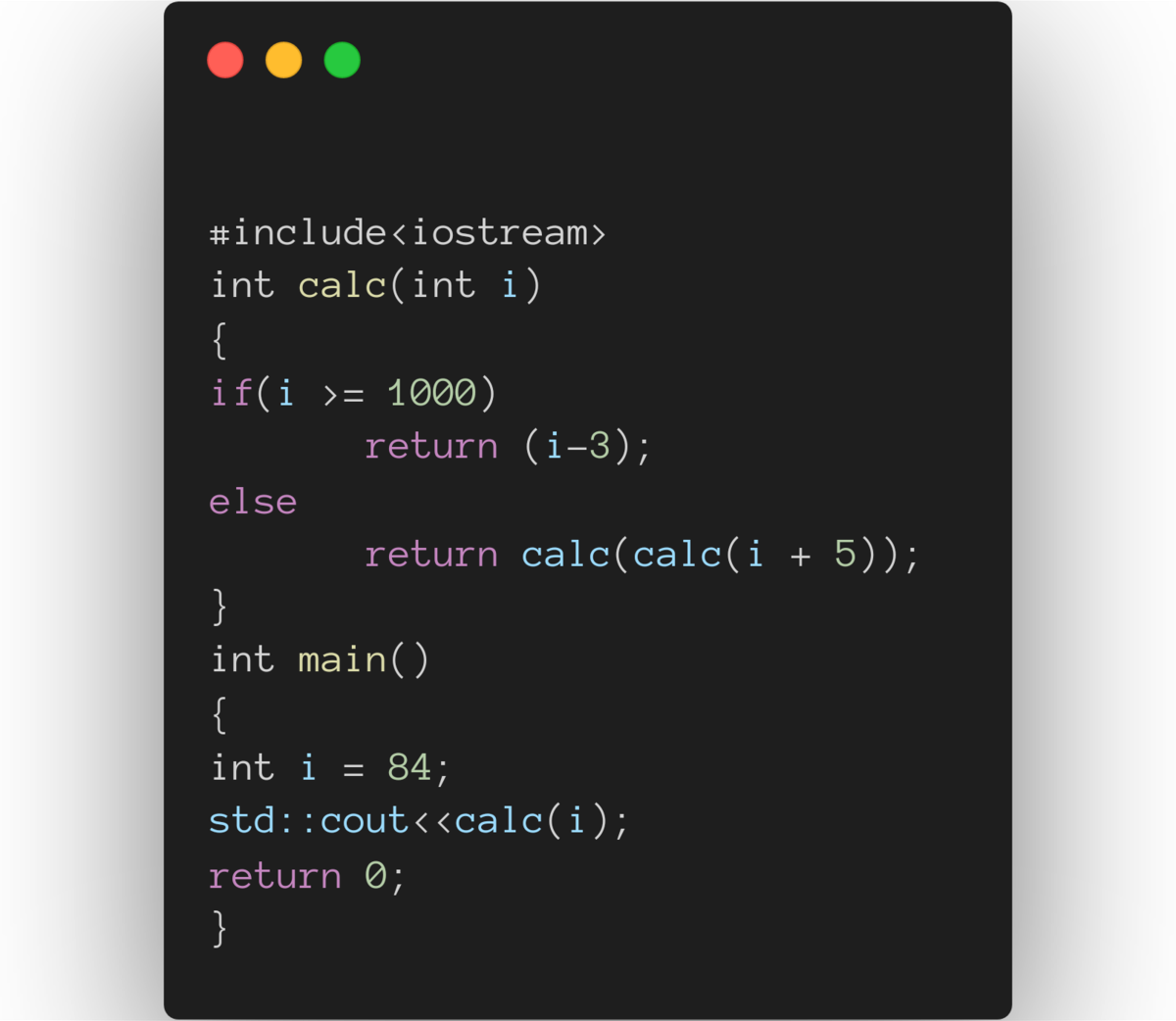 Solution using C++
Solution using C++