S-R

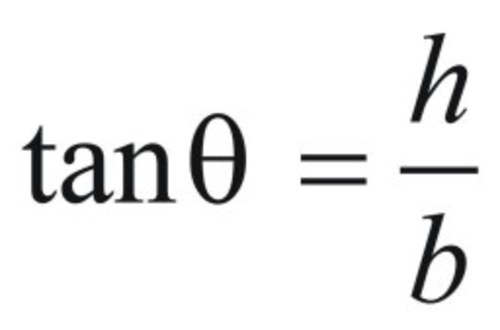Level pending

Let

S = [ t a n A / ( 1 − c o t A ) ] + [ c o t A / ( 1 − t a n A ) ] R = s e c A c s c A S=[tanA/(1-cotA)]+[cotA/(1-tanA)]\\ R=secAcscA\\

Find S-R


The answer is 1.

Soumo Mukherjee by Soumo Mukherjee , 25, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Soumo Mukherjee
Oct 17, 2014

Let t a n A = T tanA=T then

S = T 2 / [ T − 1 ] − 1 / [ T ( T − 1 ) ] = ( T 2 − T + 1 ) / T S={ T }^{ 2 }/[T-1]-1/[T(T-1)]\\ =({ T }^{ 2 }-T+1)/T

Substituting T = t a n A = s i n A / c o s A T=tanA=sinA/cosA

we get S = R − 1 S=R-1

0 Helpful 0 Interesting 0 Brilliant 0 Confused

A more simpler solution will be to substitute the value of tan ⁡ θ = s i n θ / c o s θ \tan { \theta } =sin{ \theta }/cos{ \theta } in the very beginning itself ,I stress you to do so .Because to find relation between S &R we need one in terms of other.It will be wise to exploit R which is much simpler in form than S .So,we need to write S in terms of R.Now R is already in terms of s i n θ sin{ \theta } & c o s θ cos\theta i.e in simplest form,therefore I recommend to solve it by substituting tan ⁡ θ = s i n θ / c o s θ \tan { \theta } =sin{ \theta }/cos{ \theta } in the very beginning itself i.e. the first step of the solution .

Soumo Mukherjee - 6 years, 7 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...