Sad Looking Stars
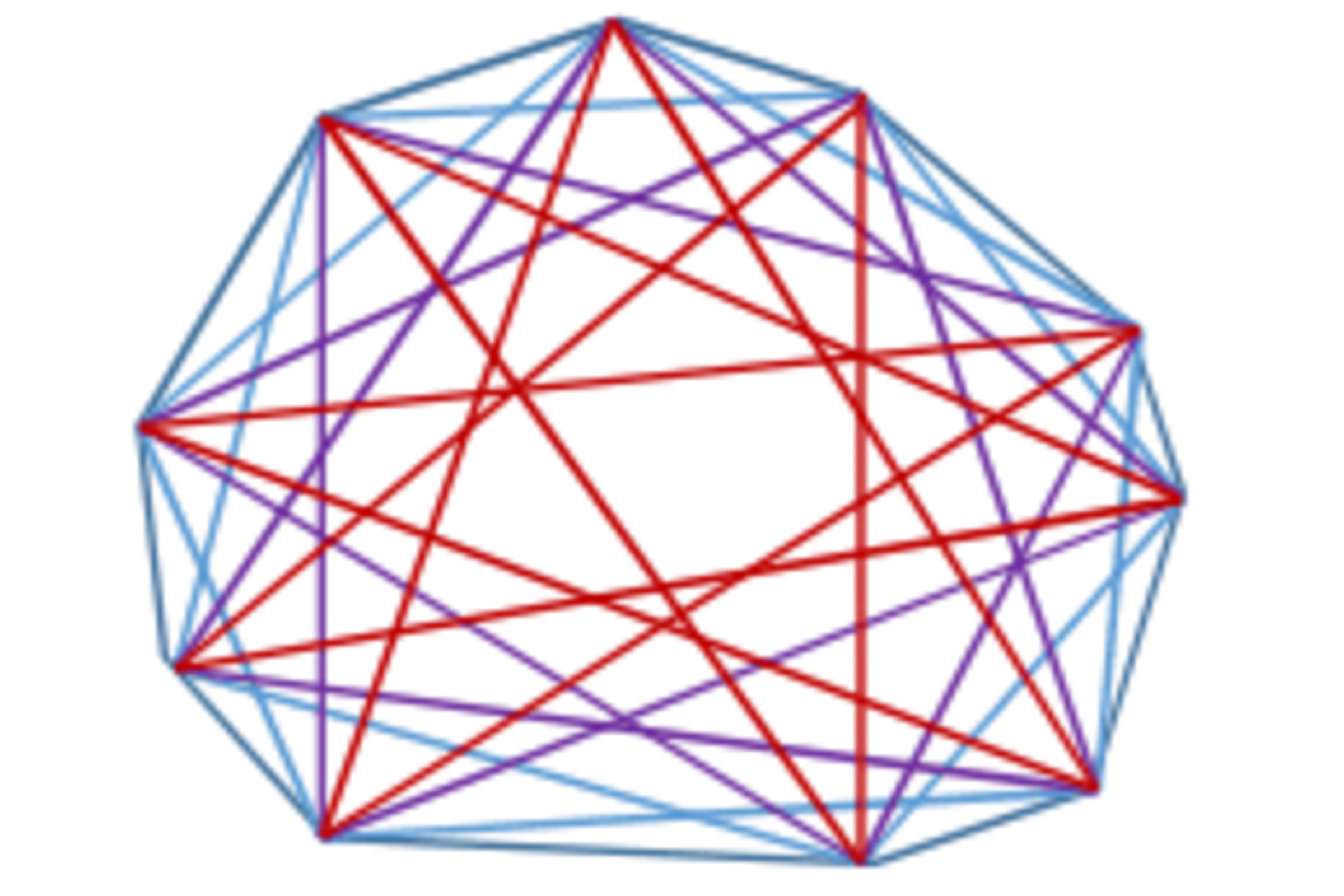
What is the average of internal angles of a convex 10-sided polygon and the stars inside of it?
Details: The first (blue) star is constructed by skipping every other vertex, and consists of two intersecting pentagons, the second (purple) star is made by skipping two vertices at a time, and the third (brown) star by skipping three at a time. The internal angles at the vertices for the polygon and the three stars, 40 in all, are the ones to be averaged. Report your result in degrees.
The answer is 90.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The sum of all the angles of the 10-sided polygon is easy: 1 0 × 1 8 0 ∘ − 3 6 0 ∘ .
The sum off the angles of the blue star is almost as trivial, if we remember that it is composed of two pentagons: 2 × ( 5 × 1 8 0 ∘ − 3 6 0 ∘ ) = 1 0 × 1 8 0 ∘ − 2 × 3 6 0 ∘ .
This pattern continues. The next star has the sum of all of its internal angles equal to: 1 0 × 1 8 0 ∘ − 3 × 3 6 0 ∘ and the last one 1 0 × 1 8 0 ∘ − 4 × 3 6 0 ∘ .
To see that this is so, let's go to the first formula, the one for the 10-sided polygon. We can derive it by adding up all the external angles and subtracting the sum from 1 0 × 1 8 0 ∘ to get the internal angles. Imagine a long rod laying on one of the sides of the polygon. Rotating it around one of the vertices it is touching until it coincides with the next segment of the polygon will make it describe the external angle at that vertex. Continue in the same direction around the next vertex, the one it came into contact with in the previous operation. This will change its angle by adding the second external angle to the first. Continue all the way around the polygon. When the rod is again on top of the same side it started on, it has rotated by the sum of all the external angles and this is equal to 3 6 0 ∘ .
A star polygon can be followed in the same way, starting with a rod coinciding with one of its segments, rotating it around a vertex at the end of that segment until it coincides with the next segment, the one starting from the end point of the previous one. Once the entire star is followed through, the rod would rotate a whole number of times. For a start made by skipping two vertices, for example, this would be three times - first time only every third vertex will be used, the second time again every third making it two out of three used by the end of second trip around, and finally the remaining vertices will be used on the third trip through. So the purple star on the diagram will have a sum of its angles equal to 1 0 × 1 8 0 ∘ − 3 × 3 6 0 ∘ .
This will be true whether a star is a single self-intersecting polygon or a combination of several of them. The brown star, for example, is made of two pentagrams with a sum of angles 2 × ( 5 × 1 8 0 ∘ − 2 × 3 6 0 ∘ ) = 1 0 × 1 8 0 ∘ − 4 × 3 6 0 ∘ .
So the totals to be added are: Polygon with 8 × 1 8 0 ∘ , first order star 6 × 1 8 0 ∘ , next 4 × 1 8 0 ∘ , and finally 2 × 1 8 0 ∘ . First and last add up to 1 0 × 1 8 0 ∘ , as do the second and the next to the last. So the average will be 1 0 × 4 2 × 1 0 × 1 8 0 ∘ = 9 0 ∘ as we have to divide by the number of angles per object and by the number of objects.
This is a general result and will hold for any even number of sides. There will be pairs adding up to n × 1 8 0 ∘ . The average will then be for each pair 2 × n n × 1 8 0 ∘ = 9 0 ∘ .This will either exhaust the number of stars, or if there is one left over, it will be in the middle and made up of quadrilaterals, so that it will by itself have an average angle of 9 0 ∘ . The result will not hold for polygons with odd number of sides, or if degenerate stars with internal angle of zero are permitted.