Sailboats in the Night
The triangle in this figure has side lengths 3, 4, 5. The arcs within the circle are semicircles.
What is the total area of the regions in blue?
The answer is 12.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
11 solutions
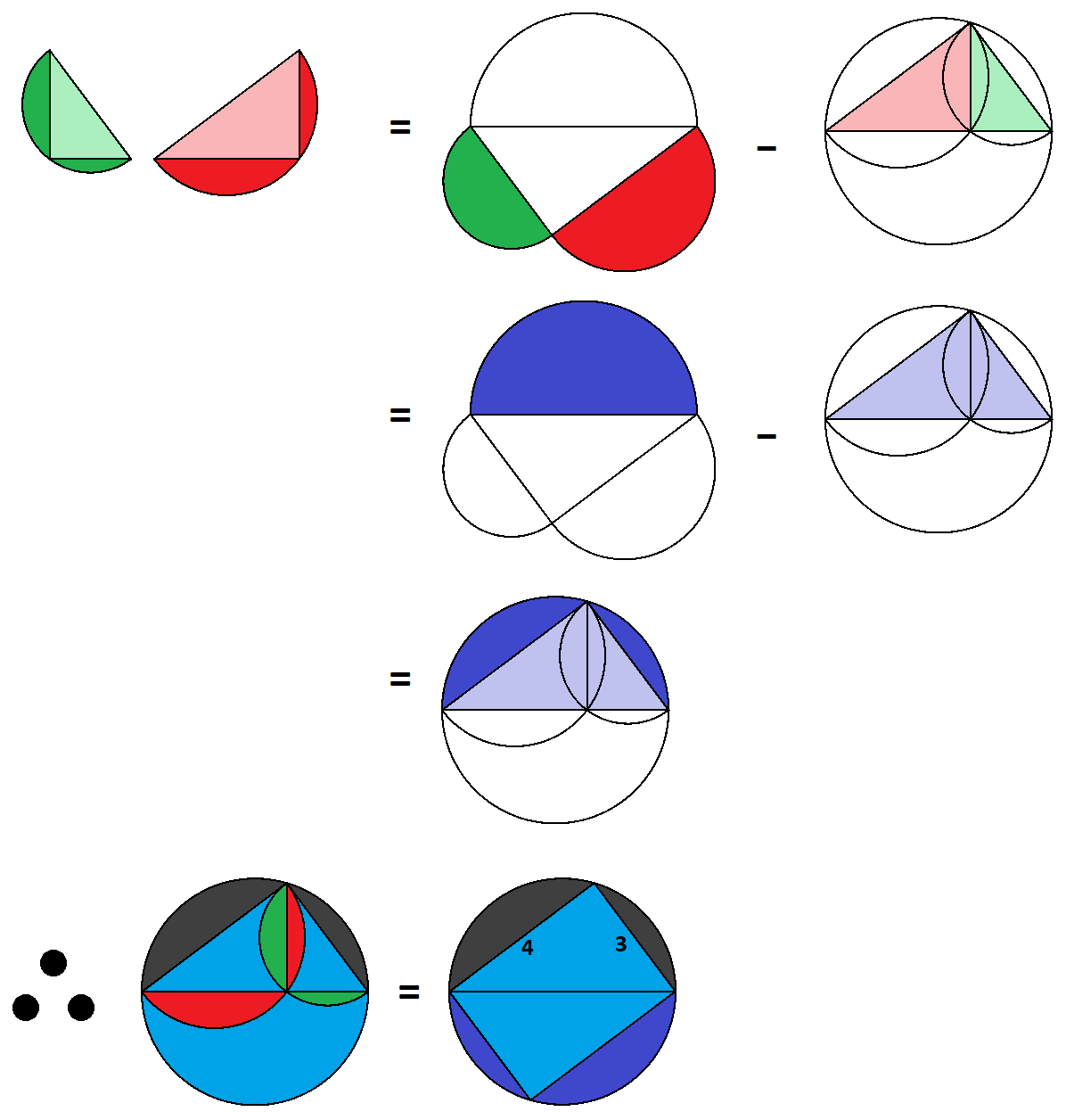
Thanks, Albert, for posting such a pretty picture proof, showing that the sum of the green and red areas is the same as the sum of the blue areas. Math can be art.
Log in to reply
thanks! this is a beautiful problem too.
Beautiful and most elegant of all the solutions shown. Reminds me of the Japanese Sangaku puzzles. I completely didn't think of the pythagorean idea of semircles. I thought of the red and green part of the proof completely separately from the blue, and worked hard for the numbers to strenuously get the answers for the separate parts and combined them to get the answer, but never thought of that they are one and the same. I learned much from you solution. Thank you for posting it.
I have still not understood the - operation.. Can someone give me clarity
I applied 2 layers of paint to the triangle and 1 layer of paint to the large semicircle. Then I applied 1 layer of paint thinner to each of the smaller semicircles. The result was identical to the initial picture.
Then I realized the area of a semicircle is proportional to the square of diameter, and per the Pythagorean theorem, the areas of the smaller semicircles add up to the large semicircle. So the paint and the paint thinner in the semicircles cancel each other out exactly.
Therefore, the amount of paint left was the equal to the 2 layers of paint over the triangle and 2 * 3 * 4 / 2 = 12.
Now I feel dizzy after inhaling all the paint thinner.
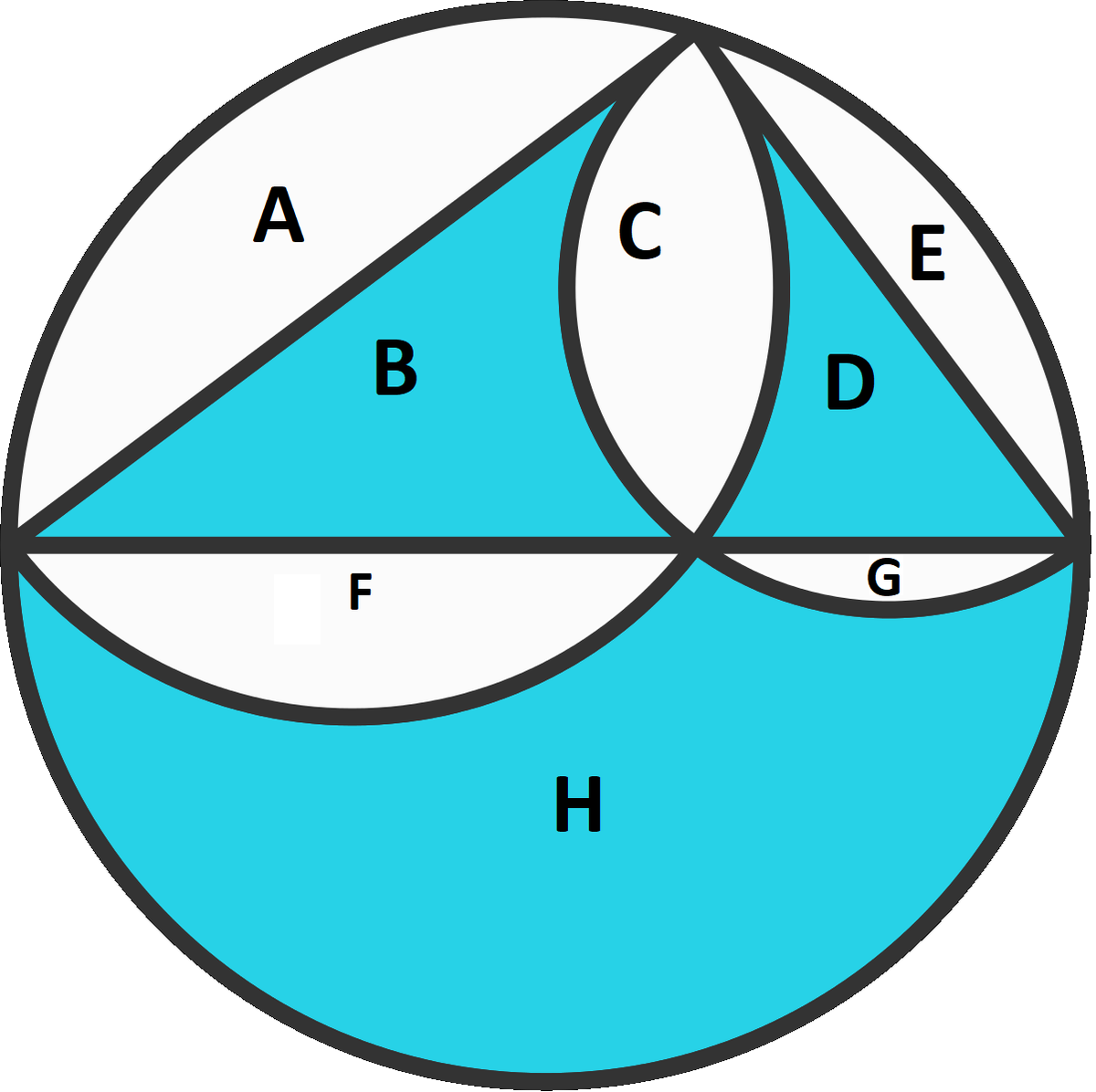 B
+
D
+
H
=
?
B
+
D
+
H
=
?
Solution:
B + C + F = 2 π . . . ( 1 )
D + C + G = 8 9 π . . . ( 2 )
F + G + H = 8 2 5 π . . . ( 3 )
B + C + D = 6 . . . ( 4 )
2 ( 4 ) + ( 3 ) − ( 1 ) − ( 2 ) yields,
B + D + H = 1 2
I like this proof!
Shouldn't the coefficients for pi be 2, 9/8, and 25/8 rather than 4, 9/4, and 25/4?
Or using your letters. (1) is area of first half circle H1 = B+C+F. (2) os H2=D+C+G. And (3) H3=F+G+H. And (4) area of triangle T=B+C+D.
Note H3+T is the are of the triangle and the biggest half circle. The blue area = (H3+T)-(white area inside H3+T). But notice that (area of white parts inside H3+T)=H1+H2-T. So blue area = H3+T-(H1+H2-T)=2T+(H3-H1-H2). But by pythagoras theorem H3=H1+H2. So blue area =2T=2 (4 3/2)=12.
Let the area of the 3 , 4 , 5 triangle be A = 6 , and let the areas of the semicircles of diameters 3 , 4 , 5 be A 3 , A 4 , A 5 , while the area of the circle is 2 A 5 . Then the total area of the [white] regions are
A 3 + A 4 − A plus A 5 − A
But since 3 2 + 4 2 = 5 2 so that A 3 + A 4 = A 5 , the total area of the [white] regions are 2 A 5 − 2 A . Therefore the total area of the regions in cyan is 2 A = 1 2 .
This problem is very tricky, but my other considerable problem was that I cannot understand your sentence "The triangle in this figure has sides 3, 4, 5.". I have not had my mathematics education in English and so I am unfamiliar with the terminology you are using. Is "3, 4, 5" referring to the lengths of the sides? As in Height = 3 Units, Length = 4 Units and Hypothenuse = 5 Units?
Log in to reply
Yes, a triangle with side lengths of 3, 4, 5, which is a famous Pythagorean triple, i.e., 3 2 + 4 2 = 5 2 .
I've fixed the wording so that hopefully it'll be clearer.
Execllent solution! In fact,the colors of the regions are also interference factors.
What black regions are you talking about? I only see cyan and white regions in the original image...
Log in to reply
picture was changed by the Brilliant Staff... let me reword my solution
(1) is area of first half circle H1 = B+C+F. (2) os H2=D+C+G. And (3) H3=F+G+H. And (4) area of triangle T=B+C+D.
Note H3+T is the are of the triangle and the biggest half circle. The blue area = (H3+T)-(white area inside H3+T). But notice that (area of white parts inside H3+T)=H1+H2-T. So blue area = H3+T-(H1+H2-T)=2T+(H3-H1-H2). But by pythagoras theorem H3=H1+H2. So blue area =2T=2(43/2)=12
I came to my solution by considering things in terms of superpositions of basic shapes. Imagine two types of overlapping areas which cancel each other out when they overlap the same section. You get a blue section when one kind has one more overlap than the other kind. You get a white section when they have the same number of overlaps. Using this approach, if you had two positive triangles, and a large positive semicircle, as well as two negative semicircles partially overlapping the triangle, you would get the diagram shown. If you add the positive shapes areas and subtract the negative shapes you get 12.5pi + 6 + 6 - 8pi - 4.5pi = 12.
I labeled all areas, a-e from left to right in the upper half and g-h in the lower half. Almost the same as Tolga did(only swapping g and h).
The area of five regions is known:
W = f + g + h = 8 2 5 π (lower half circle with radius 5/2)
X = a + b + c + d + e = 8 2 5 π (upper half circle with radius 5/2)
Y = b + c + f = 2 π (half a circle with radius 2)
Z = c + d + h = 8 9 π (half a circle with radius 3/2)
T = b + c + d = 6 (area of triangle)
I am looking for a linear combination of these known regions that is just the asked area
A = b + d + g
Since g is only in W, I need region W once. Now because W= f+g+h, we want to get rid of f and h, so subtract Y and Z (which are the only regions left containing them). We now have W-Y-Z=g-b-2c-d. Adding 2T will do the trick: W-Y-Z+2T= g-b-2c-d+ 2(b+c+d)=g+b+d
A = b + d + g = W − Y − Z + 2 T = 8 ( 2 5 − 1 6 − 9 ) π + 1 2 = 1 2 .
Only now I see that W=Y+Z and feel stupid, because I realize it probably was even simpler.
Note. I and many others just assumed that the point where the circles cross is exactly on the edge of the triangle. Let's check that. By symmetry, this point must be below the top of the triangle. Dropping a line from the top, we create two new triangles of the same ratio 3:4:5. Using these ratios, we see that our point is 16/5 from the left and 9/5 from the right, and also that the height of the triangle is 12/5. So relative to our point, the circles have centers at (-1.6,1.2) and (0.9,1.2). The distances then are ( − 1 . 6 ) 2 + ( 1 . 2 ) 2 = 2 and ( 0 . 9 ) 2 + ( 1 . 2 ) 2 = 1 . 5 , which are indeed the expected circle radii.
It’s a little difficult to calculate just the blue area without including the three pairwise intersections of the three semicircles (C,F & G in Tolga Gürol’s diagram above), but it’s easy to calculate the area including these intersections either once (call that area X), or counting them twice (call that area Y). Then the blue area will be 2X - Y.
If Z(n) is the area of a circle of diameter n,
then Y = (Z(5) + Z(4) + Z(3))/2, that is, just adding up the areas of the three semicircles
and X = (3*4 + Z(5))/2, because we know the triangle in the problem is a right triangle, and you just combine that area with the area of the largest semicircle.
Then 2X - Y = 12 + (Z(5) - Z(4) - Z(3))/2
But it is easy to show that Z(3) + Z(4) = Z(5) using the formula for the area of a circle (although the intuition comes from the fact that we started out with a right triangle).
So the second term — everything but the 12 — is equal to zero, and the answer is 12.
Let
T
=
area of the
3
,
4
,
5
triangle,
W
=
area of the white bits inside of the blue area,
A
=
area of the bottom semicircle.
Using the relationship of areas of the sides of a right triangle, we have that – the sum of the 2 smaller semicircle areas =
A
.
We can then notice that – the sum of all semicircles
=
2
A
=
T
+
A
+
W
.
W
T
+
A
−
W
=
A
−
T
=
2
T
=
1
2
I came up with a solution but rounded it off to be an integer. I indicated the point where the right angle of the triangle to be the origin of a cartesian plane, expressed the semicircles in their respective equations, solved for their intersection, then integrated to certain bounds to find the area. Based on my answers in my calculator (I didn't round off in any of my steps), I got 11.78654562, yet I rounded it off to 12 to get the final answer. Seems weird that it worked.
Really weird
To calculate the area of the blue region, you calculate the area of the white region and subtract it from the area of the big circle. Area of two upper segments =area of semi circle - area of triangle =3.125Π - 6 By calculation the remaining white region is 3.125Π - 1.2x - 12.5y where x+y =5 (diameter of circle) Therefore,the area of the whole white region is 3.125Π - 6 +3.125Π - 1.2x - 1.2y Simplifying, we get 7.63495 Area of big circle is 25Π = 19.63495 So area of blue region is 19.63495 - 7.63495 =12.0
Area of big circle is 25Π =78.5398. Is an incorrect statement Area = pie r square . r = 2.5 ; 2.5 sq =6.25 so area = 6.25 x 3.14=19.634 sq inches
From the area of three semi-circles of diameters 3,4 and 5, subtract two times the area of triangle giving white area = (25π-48)/4. Subtracting the above white area from full circle area of diameter-5 (25π/4) gives the blue area as the Answer=12
Albert Lau well you could make it that simple or you could split it up in segments and need a lot longer
picture proof: