Sailing Against The Wind

Calculus Level 3

It is possible for ships to move upwind using only the power of the wind itself, using a process called tacking. It requires a movable sail and a keel that prevents the ship from sliding.

Because the keel keeps the ship from moving sideways, only forces along the boat's axis will actually push the boat. By orienting the sail correctly, the projection of the wind's force onto the sail—which is then projected onto the axis of the ship—can create a movement which is partially in the direction opposite the wind .

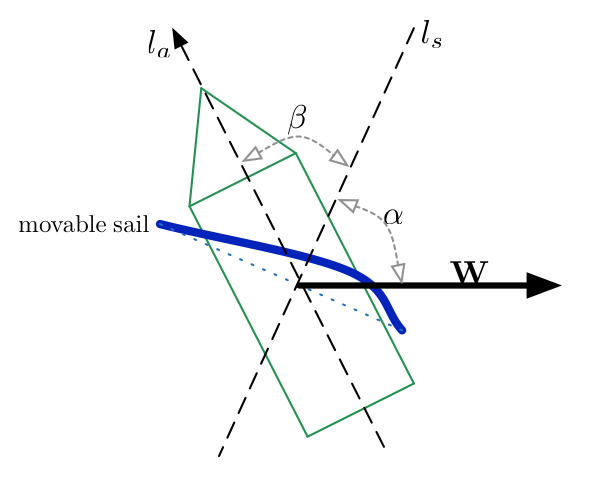
In the diagram above, $\mathbf{W}$ is the direction of the wind, $l_s$ is perpendicular to the sail and $l_a$ is along the ship's axis ( with $0 < \alpha < \pi/2,$ and $0 < \beta < \pi/2$ ).

Assuming $\alpha = \beta = \pi/3$ , what percent of the wind's force could the ship apply in the direction opposite to $\mathbf{W}$ .

33.3% 12.5% 8.1% 15.7%

1 solution

Al Imran
Mar 19, 2014

$\text{At the direction of } l_s \text{ acting force is } W\cos\alpha$ $\text{Again at the direction of } l_a \text{ acting force is } W\cos\alpha\cos\beta$ $\text{Now, at the opposite direction of W the acting force is } W\cos\alpha\cos\beta \cos(\pi-(\alpha+\beta))$ $\text{Since, }\alpha=\beta=\frac{\pi}{3} \text{ Therefore, we have }\frac{1}{8}=12.5\%$

Sailing Against The Wind

1 solution

0 pending reports