Same Height and Base
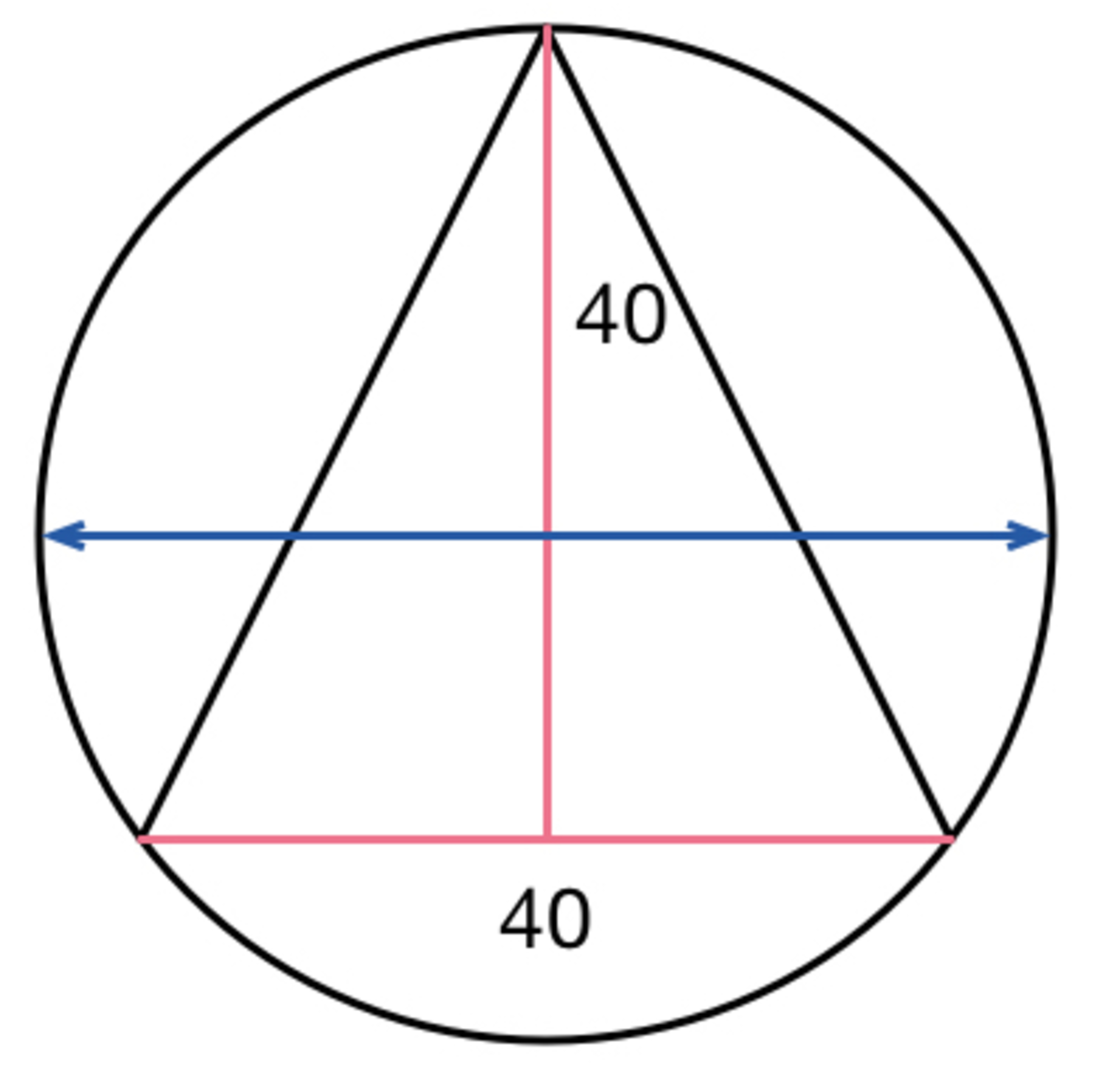
In a circle, we inscribe an isosceles triangle of base length 40 and height of 40.
What is the diameter of the circle?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Why go for trigonometry , when you can use pure geometry .
Consider the following. We can say that the center of circle is in the altitude as,
A line from the center of a circle perpendicular to the chord bisects the chord. So, as the chord is perpendicular and bisects the base (as it's isosceles), it's the center of the circle.

tan ( ∠ A B C ) = 2 0 4 0 = 2 ∠ A B C = tan − 1 ( 2 ) ⟹ ∠ A B C = ∠ A C B = tan − 1 ( 2 ) Using angle sum property, ∠ B A C = 1 8 0 − 2 tan − 1 ( 2 ) ⟹ ∠ B O C = 2 ∠ B A C , using theorem Let AD be the perpendicular, ⟹ ∠ B O D = ∠ B A C = 1 8 0 − 2 tan − 1 ( 2 ) = 2 ( 9 0 − tan − 1 ( 2 ) ) sin ( ∠ B O D ) = O B 2 0 = r 2 0 , r is radius since O is the center of circle and B is a point on the circumference of the circle. sin ( 2 ( 9 0 − tan − 1 ( 2 ) ) ) = O B 2 0 sin ( 2 tan − 1 ( 2 ) ) = O B 2 0 2 2 + 1 2 × 2 = O B 2 0 5 2 = O B 1 0 ∴ 2 O B = d = 5 0
There is are solutions which doesn't require the use of trigonometry.
If you are familiar with power of a point , the answer follows quickly. The other algebraic approach that I can think of is to set up an equation involving pythagorean theorem . I can add that solution later.
Log in to reply
Eureka , I have posted a simple solution based on pythagoras' theorem
Label the points as above. Observe that the altitude of the isosceles triangle extends to the diameter of the circle.
Consider power of a point applied to the point O . We know that O A × O C = O B × O D .
Thus O D = 4 0 2 0 × 2 0 = 1 0 . Hence, the diameter is B D = B O + O D = 4 0 + 1 0 = 5 0 .