Same height, Largest area
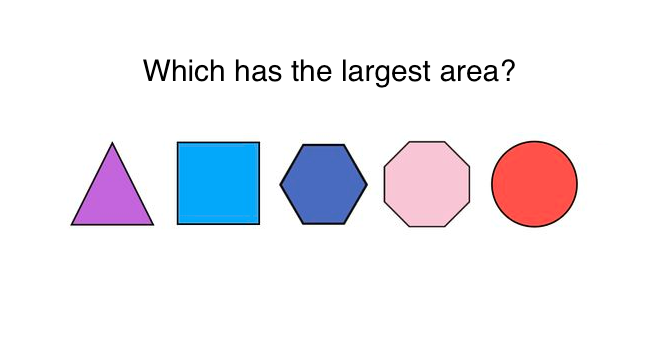An equilateral triangle, a square, a regular hexagon, a regular octagon, and a circle all have the same height. Which one has the largest area?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
The octagon and the circle can fit wholly within the square, so we can rule those out. The triangle would have to have a side length more than twice that of the square to have a greater area, which could only be the case if the base angles were 3 0 ∘ and not 6 0 ∘ as is the case with an equilateral triangle. The hexagon did concern me, so I did have to go ahead and make some calculations as you did. I can't see any obvious intuitive reason for why the square's area is necessarily greater. I calculated the area of a pentagon with the same "height", (middle of one side to opposite vertex), and found a pentagon-to-square area ratio of 5 − 2 5 ≈ 0 . 7 2 7 , which surprised me as I thought it would be more than the hexagon. Perhaps I'll look at heptagons and nonagons later. :)
Log in to reply
I found this interesting and glad you did too. What were your observations?
Just compare all the shapes..you will notice the widths(diameter in case of circle) and heights are same..square is complete in all sides and when we compare it with others we find some parts of them are missing..so that makes square a larger one
How did you find the side length for Hexagon and Octagon ?
Log in to reply
Using trigo and the height of isosceles triangle. For the hexagon, the base angle is 6 0 ∘ and the height of the isosceles triangle is 2 1 , and so the side length is 2 × h × cot θ = 2 × 2 1 × cot 4 5 ∘ = 3 3 .
The way I figured it was if all of the shapes have an equal height they can all be cut from a piece of paper the size of the square.
Log in to reply
That claim is not true. For example, in the triangle, we have a base of 3 2 > 1 , and so it cannot fit into a square of side length 1 (without some tilting).
The apothem is the (perpendicular) distance from the center to the midpoint of a side; call that r. An n-gon has n lines from its vertices to the center and n apothems; using these to break it into 2n identical right triangles, we find the area of the regular n-gon to be n r 2 tan n π . We see that this decreases strictly for increasing n. Thus, for the same apothem, the more sides we add, the more we shave off the area. (You can think of the polygons as approximations of a circle that are always too big, where that "too big" is bigger for the rougher (lower n) approximations.)
For an even regular polygon, the apothem is half the height, so all those (including the circle, which is the infinite-sided regular polygon) have the same apothem, and therefore fit the pattern above. Odd regular polygons do not have such a simple relationship between height and apothem, but we only have one of those, a triangle, which is easy to check as a special case.
Thus, either the lowest-n even polygon (the square) or the triangle is our winner; the formula for each area is well-known and simple, and checking tells us the square wins.
(I would recommend visual inspection, but the graphic is actually a non-equilateral triangle.)
Great observation!
It is interesting that the pentagon (with height 1) has a larger area than the triangle, but a smaller area than the hexagon. I'm trying to understand it, but don't see why (other than doing all the calculations).
All the other figures would fit in a square if the heights are same.
Not true. The equilateral triangle's base is 3 2 as long as its height -- that's 15% wider than the square -- for instance. (Note that the triangle in the graphic is not equilateral.)
Simple logic, no math involved. A square is as wide as it is tall. All the other shapes are sometimes as wide as they are tall, but have corners or pieces missing. Thereby, the square has the largest area.
Unfortunately, that's not true. For example, in the triangle, we have a base of 3 2 > 1 , and so it cannot fit into a square of side length 1 (without some tilting).
I got tricked by this. I wasn't expecting the answer to be the square, so let me show my working:
Let the height of the figures be 1.
Triangle: Height of 1, Base of 3 2 , Area of 2 1 × 3 2 × 1 = 3 1 ≈ 0 . 5 7 7 .
Square: Height of 1, Area of 1 2 = 1 .
Hexagon: Height of 1, side length of s = 3 3 , area of 2 3 3 s 2 ≈ 0 . 8 6 6
Octagon: Height of 1, side length of s = 1 + 2 1 , area of ( 2 + 2 2 ) s 2 ≈ 0 . 8 2 8
Circle: Height of 1, radius of r = 2 1 , area of π r 2 ≈ 0 . 7 8 5 .
I don't know why the square has the largest area, other than just checking these calculations. Any ideas?