Sammy the spider
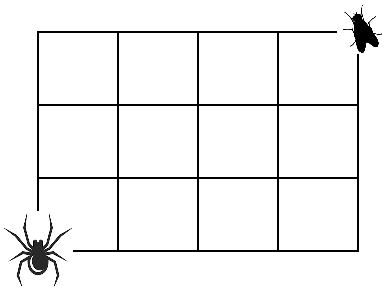
Sammy the spider has a grid web, where he rests and eats at . If he can only move up and to the right, in how many different ways can he catch a fly that lands at ?
- Credits also goes to Chew-Seong Cheong for helping me to make this question.
- Check out this set of such problems
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The general solution of this type of problem for the number of ways N ( m , n ) = ( m m + n ) = ( n m + n ) , where m and n are integral horizontal distance and integral vertical distance between the starting point and the ending point respectively. Therefore, for m = 4 and n = 3 , we have N ( 4 , 3 ) = ( 3 4 + 3 ) = ( 3 7 ) = 3 5 .
We can also solve the problem using a diagram shown above by assigning at each node of the grid the number of ways to the destination. That numbers for nodes on the top horizontal line are all 1's N ( m , 0 ) = ( 0 m ) = 1 . Similar those of the vertical line on the right N ( 0 , n ) = 1 . For the rest of the nodes, the number is the sum of the number above and the number on the right or N ( m , n ) = N ( m , n − 1 ) + N ( m − 1 , n ) . We find that all N ( m , n ) = ( n m + n ) .