Sands of Time
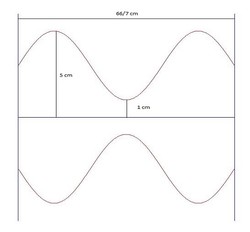The upper half of image represents a portion of sine wave from x=0 to x=3*pi which is scaled and then translated along y-axis such that the minimum distance from x-axis is 1 cm and maximum distance is 5 cm.
This curve is then rotated along x-axis to form the surface like that of a hourglass lying sideways.
Assume that an extremely thin closed hourglass with curved portion resembling this surface is filled with sand equal to half of it's volume.
The hourglass is initially kept upright with all sand in upper half portion. Given that sand particles pass through the area of cross-section separating the upper-half and lower-half of hourglass in a uniform manner with velocity equal to cm per second, After how may seconds will all the sand fall to lower-half.
(Use pi= )
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
The sine wave described is y=2sinx+3. Use the disc method to find the volume of the hourglass by way of integrating the square of this function from 0 to 3pi and multiply by pie.
Then divide the volume of the hourglass by two to find the volume of the sand; then finally divide the volume of sand by the product of the given velocity and pi (since pi is the area of the cross section which separates the upper and lower halves, aka a circle with radius 1) to acquire the final answer.