Sandwich in a Box

In the case where an entire side of the triangle adjoins a side of the box, we can justify the area is 1/2 by dividing the figure into rectangles, and noting each rectangle is subdivided by half. Essentially, each portion of "positive space" of the triangle has corresponding "negative space" of the remaining part of the box.

We can also say that the base is 1 and the height is 1 of this triangle so the area is $1 \times 1 \times \frac{1}{2} = \frac{1}{2} .$ Note that if we try to make the triangle so that the side adjoining the box is shorter the base will necessarily be smaller, so the area will have to be less than $\frac{1}{2} .$ The same issue occurs if we just try shrink the height of the triangle.

Now, suppose instead we have a scenario where one vertex of the triangle touches the corner of the box (and the sides aren't adjoining). We can again attempt to draw rectangles and match "positive space" with "negative space". There will be a rectangle left out of the matching process, as shown. In addition, one of the triangles (#2) doesn't make a perfect match; that means that particular rectangular has more "negative" rather than "positive" space. In other words, the "negative space" of the box must be larger than the "positive space" filled by the triangle.

The same is true if all the vertices of the triangle touch the sides (and there will be 2 "negative space" rectangles that are unaccounted for).

Any attempt where at least one vertex does not touch the box, we can draw a different, smaller rectangle or square around the triangle and repeat the process. Since the new box is smaller, that means, again, at least some of the "negative space" of the original box must not have corresponding "positive space".

Hence in any scenario the area of the triangle cannot be larger than $\frac{1}{2}$ the area of the box.

Formula for the area of a triangle is base x height / 2. The area of box (parallelogram) is base x height so the largest triangle will never more than half the area of any parallelogram becuse you can’t use more than it’s full height and full base. No need for pictures... it’s a simple math formula unless you want to demonstrate that using a longer base shortens the triangles height proportionally.

By a series of indirect proofs (see below), we can show that the largest triangle in a square box must share a side with the square and have a third vertex on the side of the square opposite to the shared side, which has an area half as large as the box. Therefore, a triangular sandwich larger than the one given cannot fit into the same square box.

First, assume that the largest triangle in the square box has a vertex inside the square box (not on one of the square sides or corners). But then we can take one of the sides that shares that vertex and extend it towards one of the sides of the square to create a triangle with a longer base and therefore a larger area, which contradicts our assumption. Therefore, the largest triangle in the square box must have all three vertices on the edges or corners of the square box.

Next, assume that the largest triangle in the square box has all three vertices on the edge of the square but not on the corners. Then there are two cases: a triangle with two vertices on the same side of the square, or a triangle with each of its vertices on different sides of the squares.

In the first case, if the triangle has two vertices on the same side of the square, then we can take the side of the triangle that shares part of the side of the square and extend it in both directions to create a triangle with a longer base and therefore larger area, which contradicts our assumption, which means that the largest triangle with two vertices on the same side of the square must have both those vertices in the corners of the square.

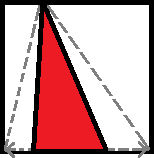
Furthermore, if the triangle's third vertex is on a side of the square not opposite to the triangle's base, it can be extended away from the base to create a triangle with a longer height and therefore a larger area, which gives us a triangle that shares a side with the square with a third vertex on the side of the square opposite to the shared side.

In the second case, if the triangle has all three vertices on different sides of the squares, then there is one side of the square that does not contain a vertex. Let $s$ be the side length of the square, $a$ be the shortest distance between the vertex of the triangle closest to the non-shared side of the square to the non-shared side of the square, $b$ be the shortest distance between the vertex of the triangle second closest to the non-shared side of the square to the non-shared side of the square, and $c$ be the shortest distance between the vertex of the triangle on the side opposite to the non-shared side of the square to the nearest corner of the square, as pictured below.

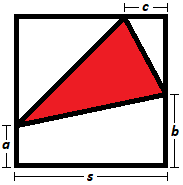
Then the area of the triangle is $A = s^2 - as - \frac{1}{2}(b - a)s - \frac{1}{2}(s - b)c - \frac{1}{2}(s - a)(s - c)$ which simplifies to $A = -(s + c)a - \frac{1}{2}(s - c)b + \frac{1}{2}(s + c)s$ , which is a decreasing linear function for positive fixed values of $b$ , $c$ , and $s$ , and so the largest area occurs when $a = 0$ ; in other words, when the vertex of the triangle is on the corner of the square. Now the area of the triangle is $A = -\frac{1}{2}(s - c)b + \frac{1}{2}(s + c)s$ , which is also a decreasing linear function for positive fixed values of $c$ and $s$ , and so the largest area occurs when $b = 0$ ; in other words, when the vertex of the triangle is on the corner of the square. We therefore once again have a triangle that shares a side with the square with a third vertex on the side of the square opposite to the shared side.

I don't know anything complicated but i know that the biggest triangle in the square is half an area of a square

The answer is No.

Because the sandwich(red triangle) is half the space of the box and the other sandwich is larger it can't fit in the box.

The largest triangle that can be formed is dividing the square by a straight line diagonally and that is the half of the square and therefore no larger triangle can be formed.

Let's assume that the biggest possible triangle in a unit square has its vertices on three different edges of the square (possibly at a shared corner), so we only need to consider such triangles. One edge of the box has no vertices (except perhaps at its ends). Lay this edge along the x-axis so that the square is in the first quadrant, and let the vertices of the triangle be at (0,a),(b,1) and (1,c) where a,b and c are non negative reals less than or equal to 1.

Now apply the shoelace formula to see that the area of the triangle is

$\frac{1}{2}\left( 1+ab-bc-a \right)=\frac{1}{2}\left( 1-a(1-b)-bc\right) \le \frac{1}{2}$

(after posting I read David Vreken's solution. His solution is much fuller than mine, justifying all the assumptions)

The largest tri.. that can be fitted inside a tri.. can possess only 1/2 the area of the sq..(check out urself) a sq.. is a parallelogram. Here,both the parallelogram and the triangle possess the same base and lie between the same parallels,so the area of the triangle is 1/2 the area of the parallelogram (acc.. to theorem) Therefore, the answer is No.