Sangaku Folding B
A 1 0 × 1 0 square piece of paper is folded as in the following figure:
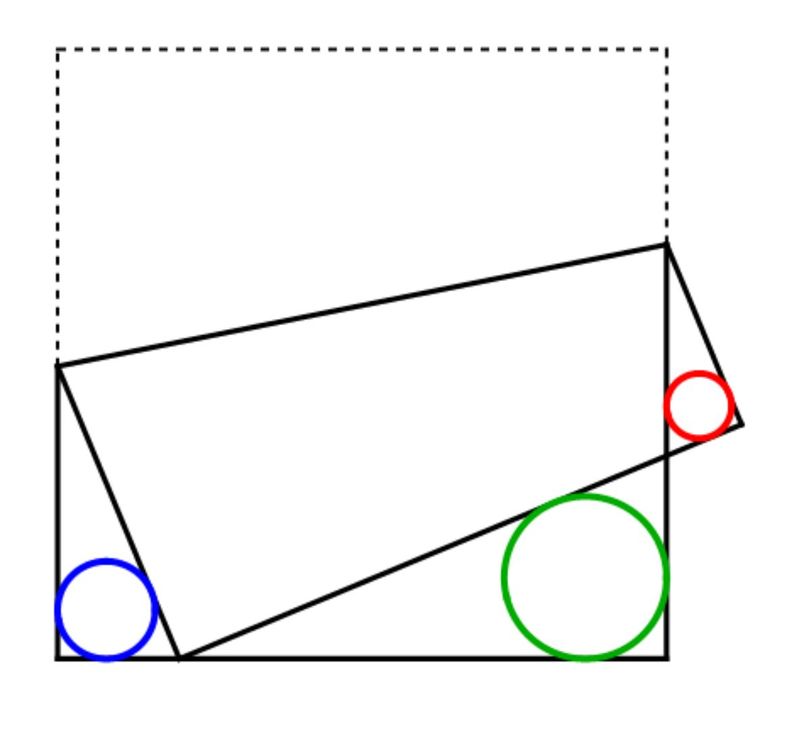
The upper left corner of the paper is folded over so that it touches the bottom edge of the paper. Three circles are inscribed in three triangles as shown in the figure.
- The blue circle has a radius of 5 4 .
- The green circle has a radius of 3 4 .
- The red circle has a radius that can be expressed as b a ,
where a and b are coprime integers. Find the sum a + b .
The answer is 23.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Sumptuous!
Log in to reply
Glad that you like the food, I mean, solution.
Thanks, Chew-Seong Cheong, for that extra proof, which is what makes this problem interesting.

Can this be taken as a solution- N0 credit to me.
Are you unable to post this other than as a comment?
Other than that, your solution looks correct to me, and, yes, it's an approach different from the others. Let me have a closer look at it.
Edit: Okay, you need to fix that cubic so that it yields q = 2 or 8. That is:
q = R b ( L + q ) ( p 1 )
will yield q = 2 or 8.
In general, for a square piece of paper, R = G − B , where ( R , G , B ) are the radii of the red, green, blue circles.
In particular,
1 5 8 = 3 4 − 5 4
Let the triangle whose incircle is the blue circle be △ A B C right angled at A . Let ∣ B A ∣ = x , ∠ A B C = α . Then x = 1 + cos α 1 0 cos α , and radius of the blue circle is 5 4 = 1 + sec α + tan α x tan α . Substituting for x , we get cos α = 1 3 1 2 , sin α = 1 3 5 , tan α = 1 2 5 , sec α = 1 2 1 3 . Let the triangle whose incircle is the red circle be △ E F G right angled at F and ∣ G F ∣ = y . Then y = 1 + cos α 1 0 ( 1 − sin α ) = 5 1 6 . Then radius of the red circle is 1 + sec α + tan α y tan α = 1 5 8 . So a = 8 , b = 1 5 and a + b = 2 3
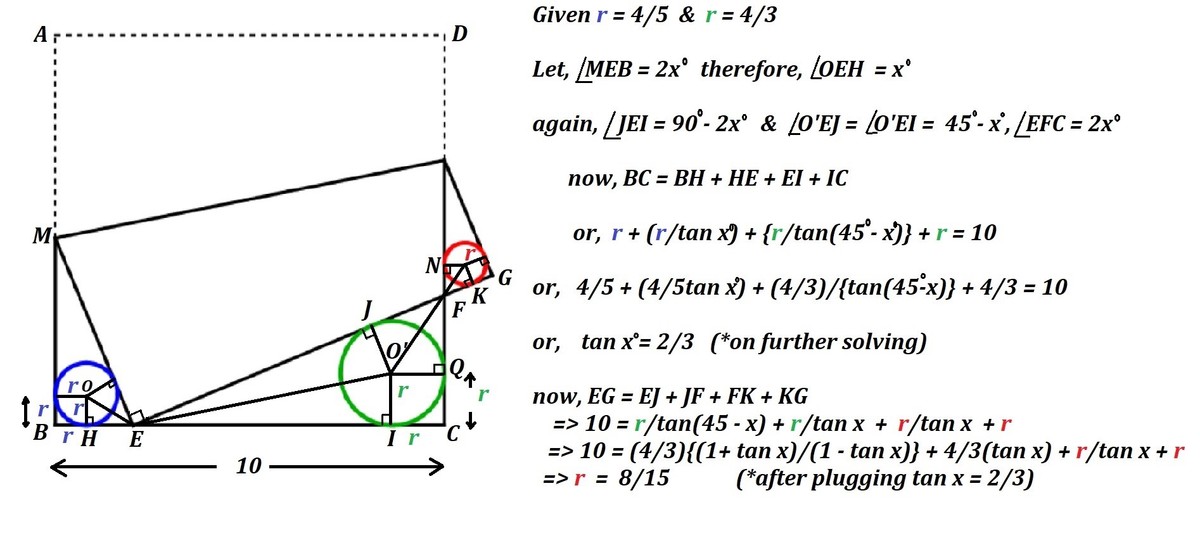
Label the figure as above. We note that △ A B C , △ C D E , and △ E F G are similar. Let A C = p and C A = q . Then p + q is the side length of the square paper. Then
A B C D ⟹ C D p + q − p 2 − q 2 3 p − 2 q q ( 1 3 q − 1 2 p ) ⟹ q p = r b r g = 5 4 × 4 3 = 3 5 = 3 5 q = 3 5 q = 3 p 2 − q 2 = 0 = 1 2 1 3 where r g and r b are radii of green and blue circles respectively. Square both sides and rearrange.
For ease of computation, let p = 1 3 and q = 1 2 and hence p + q = 2 5 instead of 1 0 . The B C = 1 3 2 − 1 2 2 = 5 , C D = 2 5 − 5 = 2 0 , C E = 2 0 × 1 2 1 3 = 3 6 5 , and E G = 2 5 − 3 6 5 = 3 1 0 . Then the radius of the red circle:
r b r r ⟹ r r = 5 3 1 0 = 3 2 = 3 2 r b = 3 2 × 5 4 = 1 5 8 .
Therefore a + b = 8 + 1 5 = 2 3 .
Bonus: General solution as mentioned by @Michael Mendrin
Since △ A B C , △ C D E , and △ E F G are similar, the ratio of the radii of the three circle r b : r g : r r = B C : D E : E G . Let ∠ B A C = θ and p = 1 ; then q = cos θ and the side length of the square paper is 1 + cos θ . Then B C = sin θ , C D = B D − B C = 1 + cos θ − sin θ , C E = cos θ C D = sec θ + 1 − tan θ , E G = C G − C E = cos θ − sec θ + tan θ , and
D E ⟹ D E − B C = C E sin θ = tan θ + sin θ − sec θ + cos θ = E G + B C = E G
Therefore r r = r g − r b .