Sangaku Jumble A
A square, an equilateral triangle, and two circles are inscribed inside a right triangle as follows:
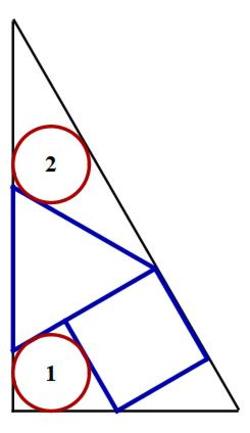
If the radius of circle 1 is 1 , what is the radius of circle 2 ?
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
I like to think that whenever we find something so "neat" as circles being of the same size, there probably has to be an underlying simple reason for it. Your figure suggests the reason in terms of symmetry.
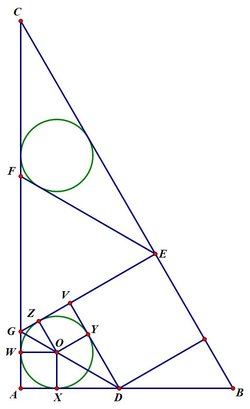Angle-chasing, we see that
B
A
C
,
O
X
D
,
O
Y
D
,
G
Z
O
,
G
W
O
are all similar right-angled triangles with the other angles being
6
0
∘
and
3
0
∘
. Thus
G
V
=
Z
V
+
G
Z
=
1
+
3
1
and
V
E
=
V
D
=
V
Y
+
Y
D
=
1
+
3
, so that
G
E
=
2
+
3
+
3
1
=
3
2
(
2
+
3
)
.
Now
C
E
F
is a
1
2
0
∘
,
3
0
∘
,
3
0
∘
isosceles triangle. If
F
E
=
x
, then this triangle has semiperimeter
s
=
2
1
x
(
2
+
3
)
and area
A
=
4
1
x
2
3
,and hence has inradius
s
A
=
2
(
2
+
3
)
x
3
Given the actual value of
F
E
, we deduce that the second circle has radius
1
.
nice approach!
Keep working going from bottom to top and finally show it is unity, very funny?
Very interesting question again! I do not have a solution, just a variation on a topic.