Sangaku Problem
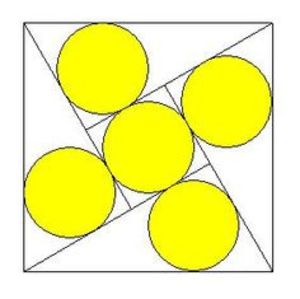
Five identical circles are arranged inside a unit square as shown in the above figure. If the radius of each of this circles is given by r = c a − b , where a , b , and c are integers with a being square-free, then find a + b + c .
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Without the circles, this is a classic proof of Pythagoras' theorem; in this vein, let the shorter sides of the right-angled triangles be u > v .
The side of the smaller central square is then u − v ; but, from the diagram, this is also 2 r .
The inradius of a right-angled triangle with sides x , y , z is r = 2 x + y − z ; so in this case r = 2 u + v − 1 . Hence 2 r = u − v = u + v − 1
so that v = 2 1 .
Also, u 2 + v 2 = 1 , so u = 2 1 3 .
Finally, r = 4 1 ( 3 − 1 ) giving the answer 8 .
Code I made which works on https://www.khanacademy.org/computer-programming/new/pjs I know, it's poorly commented, I am just throwing it here SHOULD NOTE I also have a ton of scratch-paper I used to work this out too, as well as wolframalpha for some of the trigonometric equations
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
|
And here is an interesting generalisation.
Let the radius of the circle be r and the smallest angle of the four congruent right triangle be θ . We note that 2 r + 4 r cos θ = 1 ⋯ ( 1 ) (the blue line) and sin θ + 2 r = cos θ ⋯ ( 2 ) (the short leg + 2 r = the long leg of the right triangle.
From ( 2 ) : 2 r = cos θ − sin θ . Substitutes in ( 1 ) :
( cos θ − sin θ ) ( 1 + 2 cos θ ) cos θ − sin θ + 2 cos 2 θ − 2 sin θ cos θ cos θ − sin θ cos θ − sin θ cos ( θ + 4 5 ∘ ) θ + 4 5 ∘ 3 θ ⟹ θ = 1 = 1 = 2 sin θ cos θ − 2 cos 2 θ + 1 = sin 2 θ − cos 2 θ = sin ( 2 θ − 4 5 ∘ ) = cos ( 1 3 5 ∘ − 2 θ ) = 1 3 5 ∘ − 2 θ = 9 0 ∘ = 3 0 ∘
From ( 2 ) : 2 r = 2 3 − 2 1 ⟹ r = 4 3 − 1 . Therefore a + b + c = 3 + 1 + 4 = 8 .