Santa's Mischievous Elves
Santa has 5 elves in a line named Angel, Buster, Cinnamon, Dash, and Evergreen (designated A, B, C, D, and E) who were each assigned to wrap a present 1, 2, 3, 4, and 5. They each truthfully state the following:
A:
"I wrapped a present with a number less than or equal to 3."
B:
"I wrapped an even-numbered present."
C:
"The elf that wrapped my assigned present was working next to me."
D:
"Santa assigned Angel to wrap present 1, Buster to wrap present 2, Cinnamon to wrap present 3,
me
to wrap present 4, and Evergreen to wrap present 5."
E:
"Teehee!
None of us
wrapped the present we were assigned!"
Each elf stands behind the present that he or she wrapped. Santa has to deliver present 1 to a child. Which elf's present should he deliver?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
13 solutions
Brilliant solution, and well explained with diagrams, (and the way that I usually go about this type of problem).
This is a genius solution! (How did you make the diagrams? What software?)
Log in to reply
I used Microsoft Word to make the tables, and then took screenshots and cropped the images
How 5 is must to be wrapped by C?
Log in to reply
5 must be wrapped by C because that elf hasn't yet wrapped any gift and all were assigned the work
to wrap a particular gift box
At that point Elf C is the only elf available to wrap Present 5. (Elf A did not because she wrapped a present less than or equal to 3, we already determined that Elf B wrapped Present 4 and Elf D wrapped Present 3, and Elf E did not because none of the elves wrapped a present they were assigned.)
Whoa! Sixty upvotes!
I am very impressed by the way you broke than the solution. Well done, and very well understood. Thanks.
Very good solution.
Holy Moly!!! 101 upvotes!
My favourite type of problem and solved it in the same order. Great explanation
A
didn't wrap present 1 (they wrapped different present than they're supposed to) or 3 (
C
said that his present is wrapped by the elf working next to him) . The only possibility is
A
wrapped present 2 .
So ,
B
wrapped present 4 (since he wrapped even numbered present and
A
wrapped present 2) .
E
couldn't have wrapped present 2,4,or 5 . He also couldn't have wrapped present 3 (
C
said that his present is wrapped by the elf working next to him) . The only possibility is
E
wrapped present 1 .
C
's present , 3 , must be wrapped by
D
, and
C
wrapped present 5.
So ,
E
wrapped present 1 .
Ummmmm maybe change lines a bit more often
I also followed the same procedure while solving on my own but you also explained pretty well.
A can only wrap present 2 or 3
(because 4 and 5 are numbers bigger than three and A cannot wrap present 1 because that was the present that he/she was originally assigned to.)
B can only wrap present 4
(because he cannot wrap present 1, 3 and 5 because those are odd numbers but he cannot wrap present 2 either because E stated that nobody wrapped the present they were assigned to.)
C can only wrap presents 1, 2, 5
(because 3 was the number that C was originally assigned to and 4 has already been taken by B )
D can only wrap present 3
(because C mentioned that the elf 🧝♀️ 🧝♂️ next to him/her was wrapping his/her original present which was 3 because we all know that B was already wrapping 4)
E can only wrap presents 1or 2
(because presents 3 and 4 has been taken already and present 5 is its original present.
Now, we can see that
A can wrap 2
B can wrap 4
C can wrap 5
D can wrap 3
E can wrap 1
So therefore, present 1 will be wrapped by E
Nice job on working through the details, Annie.
Why are you sure, that elve A is Angel, elve B is Buster, etc.? I didn‘t see any information showing that...
Start with all possibilities and cancel each out one by one.
| A | 1, 2, 3, 4, 5 |
| B | 1, 2, 3, 4, 5 |
| C | 1, 2, 3, 4, 5 |
| D | 1, 2, 3, 4, 5 |
| E | 1, 2, 3, 4, 5 |
A: "I wrapped a present with a number less than or equal to 3." -> Cancel 4, 5 for A
| A | 1, 2, 3 |
| B | 1, 2, 4, 4, 5 |
| C | 1, 2, 3, 4, 5 |
| D | 1, 2, 3, 4, 5 |
| E | 1, 2, 3, 4, 5 |
B: "I wrapped an even-numbered present." -> Cancel 1, 3, 5 for B
| A | 1, 2, 3 |
| B | 2, 4 |
| C | 1, 2, 3, 4, 5 |
| D | 1, 2, 3, 4, 5 |
| E | 1, 2, 3, 4, 5 |
C: "The elf that wrapped my present was working next to me." -> Cancel 3 for A and E. Notice: 3 has canceled out for B in the previous step. Thus D has wrapped present 3. -> Cancel 1, 2, 4, 5 for D; Cancel 3 for all other elves.
| A | 1, 2 |
| B | 2, 4 |
| C | 1, 2, 4, 5 |
| D | 3 |
| E | 1, 2, 4, 5 |
D: "Santa assigned Angel to wrap present 1, Buster to wrap present 2, Cinnamon to wrap present 3, me to wrap present 4, and Evergreen to wrap present 5." AND E: "Teehee! None of us wrapped the present we were assigned!" -> Cancel 1 for A, 2 for B, 3 for C etc.
| A | 2 |
| B | 4 |
| C | 1, 2, 4, 5 |
| D | 3 |
| E | 1, 2, 4 |
Cancel 2,4 for all other elves.
| A | 2 |
| B | 4 |
| C | 1, 5 |
| D | 3 |
| E | 1 |
This is already the answer. But to complete the table, cancel 1 for all other elves.
| A | 2 |
| B | 4 |
| C | 5 |
| D | 3 |
| E | 1 |
| Assigned by Santa | 1 | 2 | 3 | 4 | 5 |
| Elves | A | B | C | D | E |
From statement D and E , we can deduct that:
- A: Wrapped gift # 2. The elf stated that he wrapped gift number less or equal to 3. It cannot be gift #1 from statement E , and cannot be gift #3 from statement C
- B: Wrapped gift #4. The elf stated that he wrapped a gift with an even number, which can be #2 or 4#. From statement E it cannot be #2.
- D:Wrapped gift #3 From statement C , an elf next to him wrapped gift #3. It cannot be elf B since he wrapped an even numbered gift.
- E:Wrapped gift #1 We are left with gifts #1 and # 5. From statement E , it cannot be #5.
- C:Wrapped gift #5 The last remaining gift, #5
We first line up the elves in order: A B C D E. We know that D must have wrapped present number 3 because the elf who wrapped #3 must be on one side of C, and since, B wraps only even numbers, D must have wrapped number 3. Since none of the elves wrapped the present they were assigned, elf A must have wrapped present number 2 because he cannot wrap 1 or 3. This tells us that B wrapped #4 and C wrapped #5, leaving us with elf E wrapping present #1.
B wrapped an even present not his own, which must have been present 4 .
Since B or D wrapped C's present (number 3), and it wasn't B, D wrapped present 3 .
A wrapped present 1, 2, or 3. But since he did not wrap his own and D already wrapped 3, it must have been present 2 .
This leaves presents 1 and 5 for C and E; however, E cannot wrap present 5. Therefore, E wrapped 1 and C wrapped 5 .
1E 2C 3A 4B 5D is the right sequence.
That's wrong.
That is wrong because d is suppose to be wrapping number three because c mentioned that the elf next to her was wrapping her original one which was present number 3
How did you figure out this sequence?
No, the right sequence is A2 B4 C5 D3 E1.
This is wrong.
Here's what I did. We can get a lot of information from Dash. Since none of them wrapped the 🎁 that they were assigned to, obviously Angel didn't wrap it. For Angel, we know that she did not wrap presents 1,4, and 5. So she must have wrapped presents 2 or 3. However, from Cinnamon's statement we get that Dash is the one who wrapped 🎁 3. So Angel wrapped 🎁 2. Buster wrapped an even- numbered 🎁. If it's not 2, then it must be 4. So it's Cinnamon or Evergreen who wrapped 🎁 1. The only possible presents that Cinnamon can wrap are 1 and 5. Evergreen didn't wrap 🎁 5. So Evergreen wrapped 🎁 1. So 🎅 has to take the 🎁 of Evergreen. We wish you a Merry Christmas and a Happy New Year!( although it's done.)
Let's start off with the fact that each of the elves was assigned a gift, but none of them wrapped the ones they were assigned. Since Elf A was assigned Gift 1 , she did not wrap it. So you can cross Elf A off of the list for Gift 1 . Next, you get Elf B . Elf B wrapped an even gift, so it wasn't him who wrapped Gift 1 . He was assigned Gift 2 but wrapped another gift. Which gift - other than Gift 2 - has an even number? He wrapped Gift 4 , of course! Now, Elf C has an interesting story. She says that the person who wrapped Gift 3 was next to her. We know that Elf B wrapped Gift 4 , so it has to be Elf D who wrapped Gift 3 . Let's go back to Elf A . She wrapped a gift with a number less than or equal to 3. We know that Gift 3 has already been wrapped by Elf D , and Elf A could not have wrapped Gift 1 for obvious reasons. Therefore, Elf A wrapped Gift 2 . Great! We only have Gift 1 and Gift 5 left, with Elf C and Elf E . We know that Elf E was assigned to Gift 5 , so she didn't do that one. That only leaves her with Gift 1 , which means that Elf E wrapped Gift 1 . This leaves Gift 5 with Elf C . Thanks for reading! I hope you understood this question!
Starting from A, you know that the present could be 1,2 or 3. Then there is B, which present is 2 or 4. Then there is C, in order to know is assigned present we need to look to D. After D, E says that surely every present done by an elf is not the one assigned, and this is the key to the answer. This means that either B or D has present 3, but B, has said before, can olny have presents 2 or 4. This means D has present 3. This means that present 4 is B (because, between all the presents, the elf can only have 4). E can't have present 5, but neither A, because he can only have 1,2 or 3. This means that only C can have packaged present 5. Remains 1 and 2 and A and E. A can't have present 1, because of D's statesment. This means that the answer is E
A: wrapped less or equal to 3 A:1/2/3(given) B:1/2/3/4/5 C:1/2/3/4/5 D:1/2/3/4/5 E:1/2/3/4/5
B: wrapped even number A:1/2/3 B:2/4(given) C:1/2/3/4/5 D:1/2/3/4/5 E:1/2/3/4/5
lets see what D says first: D: santa assigned A to wrap 1, B to wrap 2, C to wrap 3, D to wrap 4 and E to wrap 5 A:1/2/3 B:2/4 C:1/2/3/4/5 D:1/2/3/4/5 E:1/2/3/4/5
C: the one next to me wrapped the present santa ordered me to wrap A:1/2(3 must be next to C) B:2/4 C:1/2/4/5(3 must be next to C) D:1/2/3/4/5 E:1/2/4/5(3 must be next to C) ∵ 3 is only possible in D ∴ D:3
E: non of us wrap the present santa ordered us to wrap A:2 (santa ordered A to wrap 1) B:4 (santa ordered B to wrap 2) C:1/5(2 and 4 is already wrapped by A and B) D:3 E:1(santa ordered E to wrap 5)
∴present 1 is wrapped by 5
If all the elves truthfully utters the above statements, we must look first to what has Dash has stated as the initial reference. After that, taking the statement of Evergreen as the next reference, Buster must not be the one who wrapped Present No. 2 but instead the latter must wrapped Present No. 4 as it is the only even-numbered Present remaining. Then, taking into account the statement of Cinnamon, Dash must be the one who wrapped Present No. 3, which is the original Present that must be wrapped by Cinnamon. Subsequently, according to what Angel has stated, she must not the one who wrapped Present No. 3 and Present No. 1 since Present No. 3 was already goes to Dash and Angel must not wrapped Present No. 1 as per what Dash has stated before. Meaning Angel is the one who wrapped Present No. 2 as it is the only Present with a number which is less than to 3. So, the remaining Presents are only 1 & 5. Since Evergreen must not be the one who wrapped Present No. 5, again as per what Dash stated as the initial reference, Evergreen must be the one who wrapped Present No. 1. Finally, Cinnamon must be the one who wrapped Present No. 5 as it is the only remaining Present.
So, the answer to the given Question is Evergreen.
Relevant wiki: Grid Puzzles
This problem can be solved by filling out a logic grid for elves A-E and presents 1-5.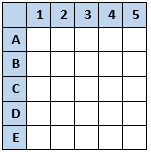 A: "I wrapped a present with a number less than or equal to 3."
A: "I wrapped a present with a number less than or equal to 3."
A did not wrap 4 or 5.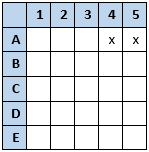 B: "I wrapped an even-numbered present."
B: "I wrapped an even-numbered present."
B did not wrap 1, 3, or 5.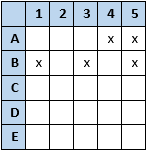 D: "Santa assigned Angel to wrap present 1, Buster to wrap present 2, Cinnamon to wrap present 3, Dash to wrap present 4, and Evergreen to wrap present 5."
D: "Santa assigned Angel to wrap present 1, Buster to wrap present 2, Cinnamon to wrap present 3, Dash to wrap present 4, and Evergreen to wrap present 5."
E: "Teehee! None of us wrapped the present we were assigned!"
A did not wrap 1, B did not wrap 2, C did not wrap 3, D did not wrap 4, and E did not wrap 5.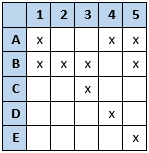 B could have only wrapped 4 (so 4 was not wrapped by anyone else).
B could have only wrapped 4 (so 4 was not wrapped by anyone else).
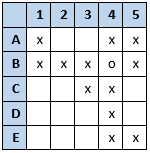 C: "The elf that wrapped my present was working next to me."
C: "The elf that wrapped my present was working next to me."
Either B or D wrapped C’s assigned present 3, but B wrapped 4, so D must have wrapped 3 (so D did not wrap any other present and 3 was not wrapped by anyone else).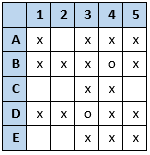 5 could only have been wrapped by C (so C did not wrap any other present).
5 could only have been wrapped by C (so C did not wrap any other present).
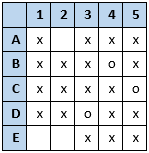 1 could only have been wrapped by E (so E did not wrap any other present), A could have only wrapped 2 (so 2 was not wrapped by anyone else.
1 could only have been wrapped by E (so E did not wrap any other present), A could have only wrapped 2 (so 2 was not wrapped by anyone else.
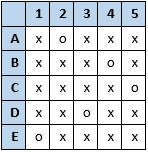 To deliver present 1, Santa should deliver E’s present.
To deliver present 1, Santa should deliver E’s present.