SAT 1000 problems - P6
Let f ( x ) = x 3 + 3 x 2 + 1 . If a = 0 , f ( x ) − f ( a ) = ( x − b ) ( x − a ) 2 , x , a , b ∈ R .
What is a + b ?
The answer is -1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
I spent hours trying to solve this problem, and couldn't. seeing the solution now makes me feel stupid.
f ( x ) − f ( a ) x 3 − a 3 + 3 ( x 2 − a 2 ) ( x − a ) ( x 2 + a x + a 2 ) + 3 ( x − a ) ( x + a ) x 2 + a x + a 2 + 3 ( x + a ) x 2 + ( a + 3 ) x + a ( a + 3 ) = ( x − b ) ( x − a ) 2 = ( x − b ) ( x − a ) 2 = ( x − b ) ( x − a ) 2 = ( x − b ) ( x − a ) = x 2 − ( a + b ) x + a b
Equating the coefficients on both sides:
{ a b = a ( a + 3 ) − ( a + b ) = a + 3 ⟹ b = a + 3 ⟹ − ( a + a + 3 ) = a + 3 ⟹ a = − 2 ⟹ b = 1
Therefore, a + b = − 2 + 1 = − 1 ,
{f(x) - f(a)} / (x-a) = (x-b) (x-a). Letting, x ->a yields f'(a) = 0. But a calculation shows f'(a) = 3a (a+2). Since a is non-zero, this means a = -2. We also know f(0) - f(a) = (0-b) (0-a)^2 = -b (4). Using the definition of f, f(0) - f(a) = f(0) - f(-2) = 1-5 = -4. Thus, -4*b = -4, or b = 1. Therefore, a+b = -2+1 = -1
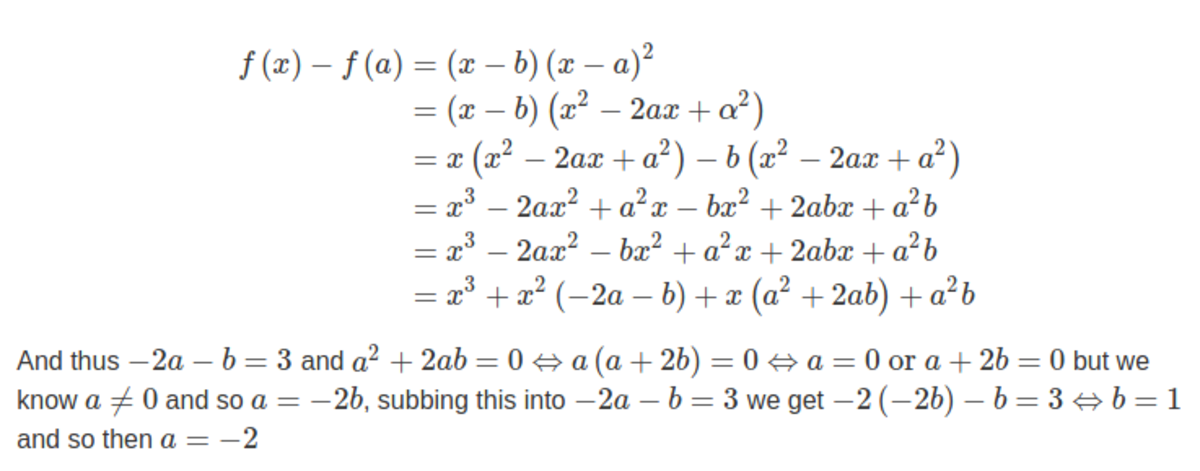
f ( x ) − f ( a ) = ( x 3 + 3 x 2 + 1 ) − ( a 3 + 3 a 2 + 1 ) = x 3 + 3 x 2 − a 3 − 3 a 2 and ( x − b ) ( x − a ) 2 = x 3 + ( − 2 a − b ) x 2 + ( a 2 + 2 a b ) x − a 2 b
Since the two expressions are equal, − 2 a − b = 3 from the x 2 terms which means 2 a + b = − 3 , and a 2 + 2 a b = 0 from the x terms which means a + 2 b = 0 .
Adding these two equations gives 3 a + 3 b = − 3 which means a + b = − 1 .