SAT Composite Figures
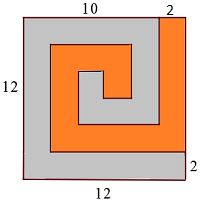 The gray and orange spirals above have a width of 2. What is the area of the gray spiral?
The gray and orange spirals above have a width of 2. What is the area of the gray spiral?
(A)
7
2
(B)
8
0
(C)
8
4
(D)
8
8
(E)
1
2
4
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Just want to show my own way to solve this. Divide the large square to 6x6 smaller squares that have area of 2x2. You'll find that gray area takes up 21 blocks. Hence, its area is (21/36) x (12x12)=84
Correct Answer: C
Solution 1:
Tip: Area of a rectangle with length
l
and width
w
:
A
=
l
⋅
w
.
We divide the gray spiral into rectangles, as shown below.
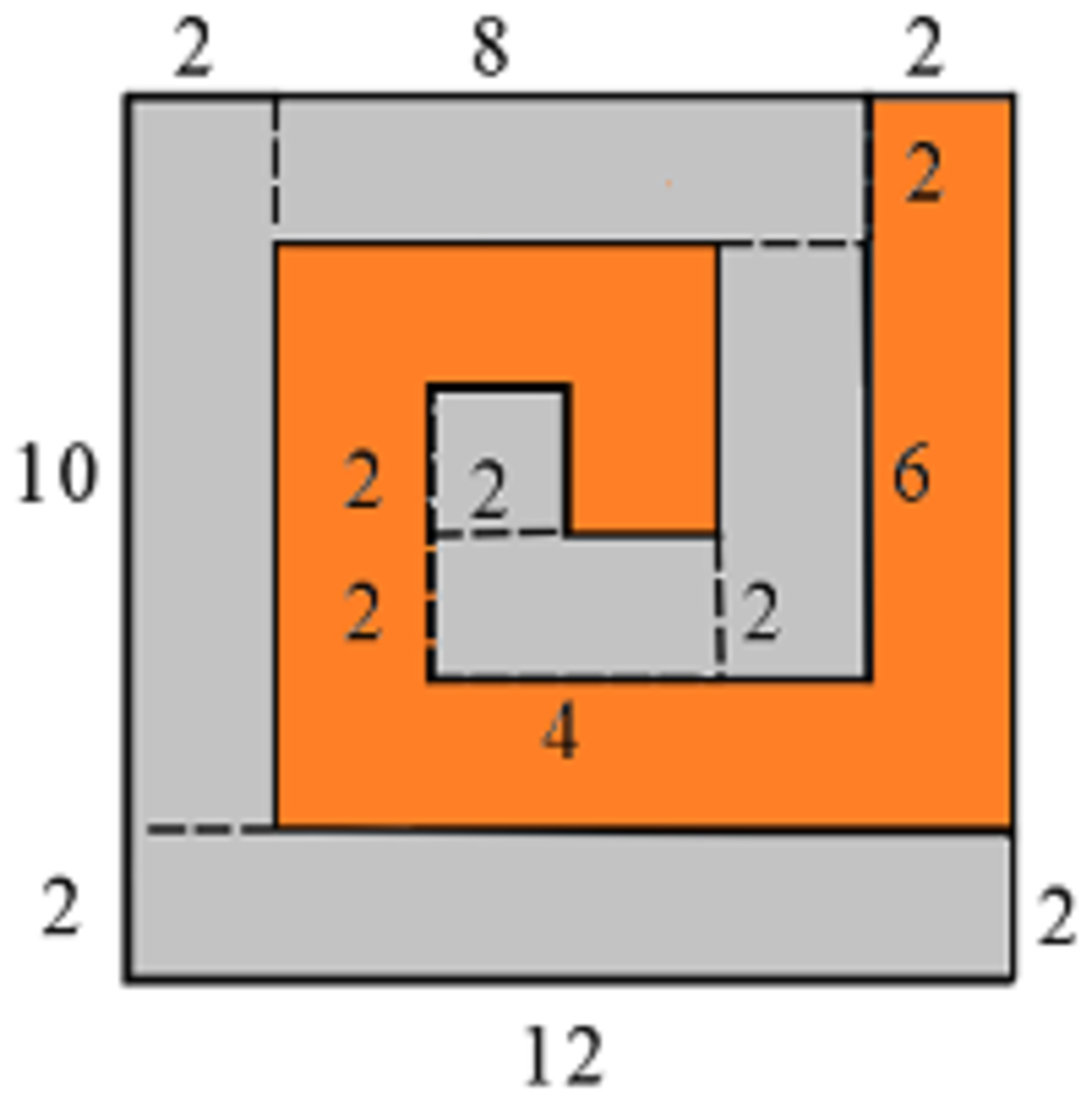
The area of the gray spiral is the sum of the areas of the rectangles.
A gray = 2 × 1 2 + 2 × 1 0 + 2 × 8 + 2 × 6 + 2 × 4 + 2 × 2 = 2 4 + 2 0 + 1 6 + 1 2 + 8 + 4 = 8 4
Solution 2:
Tip: Area of a rectangle with length
l
and width
w
:
A
=
l
⋅
w
.
Here, we subtract from the area of a square with dimensions 12 by 12 the sum of the areas of the orange rectangles.
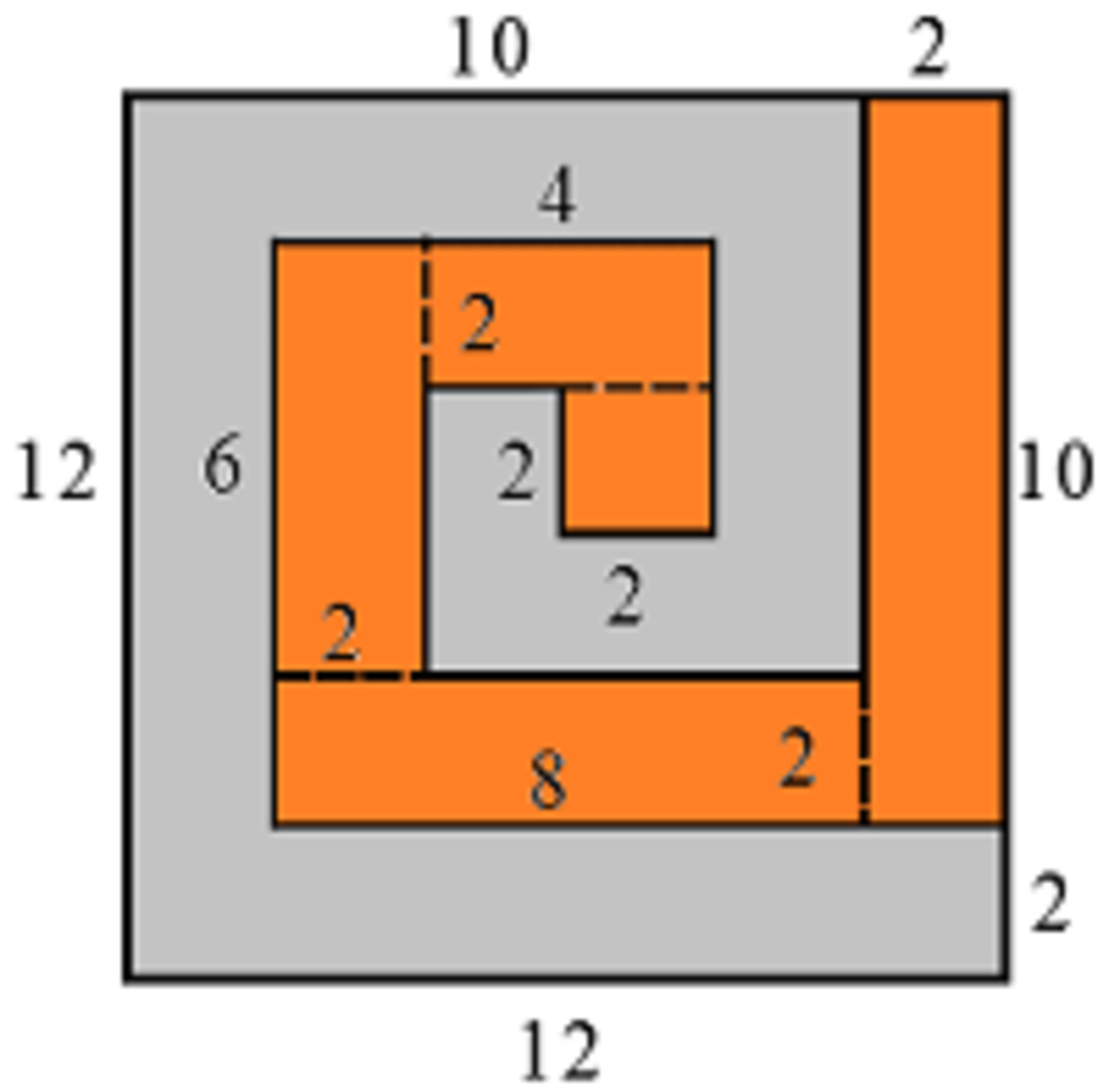
A gray = A square − A orange = 1 2 × 1 2 − ( 2 × 1 0 + 2 × 8 + 2 × 6 + 2 × 4 + 2 × 2 ) = 1 4 4 − 6 0 = 8 4 .
Incorrect Choices:
(A)
If you don't count some of the rectangles, or if you think the area of the spiral is half the area of the square with dimension 12 by 12, you will get this wrong answer.
(B)
If you don't take into account the 2 by 2 square at the tip of the spiral, you will get this wrong answer.
(D)
If you find the perimeter of the gray spiral, you will get this wrong answer.
(E)
In Solution 2, if from the area of the square with dimensions 12 by 12 you don't subtract the area of the orange rectangle with dimensions 10 by 2, you will get this wrong answer.
The measure of the spiral can be expressed as:
( 2 × 1 2 ) + ( 2 × 1 0 ) + ( 2 × 8 ) + ( 2 × 6 ) + ( 2 × 4 ) + ( 2 × 2 ) . Calculating it, we obtain the answer ( C ) = 8 4
Insert an orange 12x2 rectangle right above the figure,
then grey and orange part have equal area.
Area of the gray spiral = 2 1 4 × 1 2 = 8 4