SAT Congruence and Similarity
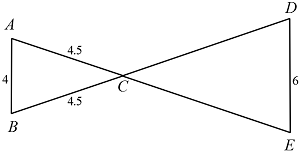 In the figure above,
and
intersects
at point
What is the perimeter of
In the figure above,
and
intersects
at point
What is the perimeter of
(A)
(B)
(C)
(D)
(E)
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Correct Answer: D
Solution:
Tip: Know how to prove triangles are similar.
We're given that A B ∥ D E . Note that B D and A E are transversals and therefore ∠ C A B ≅ ∠ C E D and ∠ C B A ≅ ∠ C D E . Since ∠ A C B and ∠ D C E are vertical angles, it follows they are congruent also.
By AAA, △ A B C ∼ △ E D C . Note that since △ A B C is isosceles, so is △ D E C .
Corresponding parts in similar triangles are proportional. So,
E D A B A B ⋅ D C D C D C D C = = = = = D C B C B C ⋅ E D A B B C ⋅ E D 4 4 . 5 ⋅ 6 6 . 7 5
Therefore, C E = D C = 6 . 7 5 .
The perimeter of △ E D C = E D + D C + C E = 6 + 6 . 7 5 + 6 . 7 5 = 1 9 . 5 .
Incorrect Choices:
(A)
If you find the length of D C or C E , you will get this wrong answer.
(B)
If you set up the wrong proportion, you may get this wrong answer. There are several ways to achieve this. Here is one example:
If you start with
D C A B = A C D E
you will get D C = 3 , and the perimeter of △ E D C = E D + D C + C E = 6 + 3 + 3 = 1 2 .
(C)
If you find the perimeter of △ A B C , you will get this wrong answer.
(E)
If you find the perimeter of the entire figure, you will get this wrong answer.