SAT Deja vu
Let A , B , C , D be points on a line in that order and A C = 1 1 , B C = 5 , B D = 6 0 . The circles with diameters A C , B D intersect at E , F . Let P be a point on the circle with diameter A D such that P , F are on the same side of A D and A P = D P . Find P E
The answer is 46.6690.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
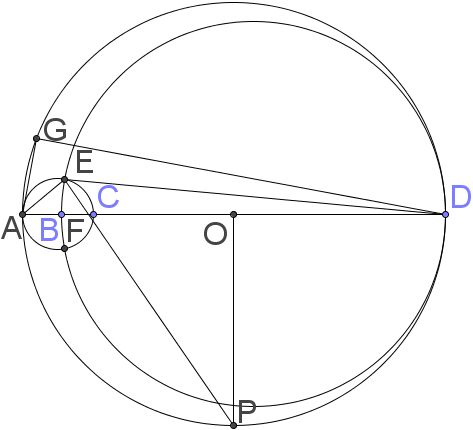 We call
O
the center of the circle with diameter
A
D
and
G
the point that satisfies that
∠
D
A
E
=
∠
E
A
G
,
∠
G
D
E
=
∠
E
D
A
and
G
is on the same side of
A
D
as
E
. Since we know that
A
P
=
P
D
, then
P
is the midpoint of the semiarc
A
D
⌢
. Similarly,
P
O
⊥
A
D
, and
A
O
=
P
O
=
D
O
, which is the radius of the circle with diameter
A
D
. We know that
B
is the harmonic conjugate of
D
with respect to
A
and
C
, because
B
C
A
B
=
5
6
=
5
5
6
6
=
B
D
A
D
. We also know that
B
E
⊥
E
D
since
B
D
is diameter, then
E
B
is the angle bisector of
∠
A
E
C
, so
∠
A
E
B
=
∠
B
E
C
=
4
5
°
, because
A
E
⊥
E
C
since
A
C
is diameter. Using the circle with diameter
A
C
, we notice that
∠
C
A
E
=
∠
C
F
E
and using the one with diameter
B
D
, we notice that
∠
E
D
B
=
∠
E
F
B
. Since
∠
C
F
E
+
∠
E
F
B
=
∠
C
F
B
=
∠
B
E
C
=
4
5
°
, we know that
∠
C
A
E
+
∠
E
D
B
=
4
5
°
. Since we defined
∠
D
A
E
=
∠
E
A
G
and
∠
G
D
E
=
∠
E
D
A
, then
∠
C
A
G
+
∠
G
D
B
=
2
∗
(
∠
C
A
E
+
∠
E
D
B
)
=
2
∗
4
5
°
=
9
0
°
. Then,
∠
A
G
D
=
9
0
°
, so
G
is on the circumference of diameter
A
D
. Since
E
is the incenter of
△
A
G
D
, then
G
E
is the angle bisector of
∠
A
G
D
, but since
P
is the midpoint of the semiarc
A
D
⌢
, then
G
P
is also the angle bisector of
∠
A
G
D
, so
G
,
E
and
P
are collinear. We know that
∠
P
A
O
=
4
5
°
, since
A
O
=
P
O
and
∠
A
O
P
=
9
0
°
, then
∠
A
E
P
=
∠
E
A
G
+
∠
A
G
E
=
∠
E
A
G
+
4
5
°
=
∠
D
A
E
+
4
5
°
=
∠
D
A
E
+
∠
P
A
D
=
∠
P
A
E
. Then,
P
A
=
P
E
=
P
D
, so
P
E
=
P
A
=
A
O
2
+
P
O
2
=
3
3
2
+
3
3
2
=
4
6
.
6
6
9
.
We call
O
the center of the circle with diameter
A
D
and
G
the point that satisfies that
∠
D
A
E
=
∠
E
A
G
,
∠
G
D
E
=
∠
E
D
A
and
G
is on the same side of
A
D
as
E
. Since we know that
A
P
=
P
D
, then
P
is the midpoint of the semiarc
A
D
⌢
. Similarly,
P
O
⊥
A
D
, and
A
O
=
P
O
=
D
O
, which is the radius of the circle with diameter
A
D
. We know that
B
is the harmonic conjugate of
D
with respect to
A
and
C
, because
B
C
A
B
=
5
6
=
5
5
6
6
=
B
D
A
D
. We also know that
B
E
⊥
E
D
since
B
D
is diameter, then
E
B
is the angle bisector of
∠
A
E
C
, so
∠
A
E
B
=
∠
B
E
C
=
4
5
°
, because
A
E
⊥
E
C
since
A
C
is diameter. Using the circle with diameter
A
C
, we notice that
∠
C
A
E
=
∠
C
F
E
and using the one with diameter
B
D
, we notice that
∠
E
D
B
=
∠
E
F
B
. Since
∠
C
F
E
+
∠
E
F
B
=
∠
C
F
B
=
∠
B
E
C
=
4
5
°
, we know that
∠
C
A
E
+
∠
E
D
B
=
4
5
°
. Since we defined
∠
D
A
E
=
∠
E
A
G
and
∠
G
D
E
=
∠
E
D
A
, then
∠
C
A
G
+
∠
G
D
B
=
2
∗
(
∠
C
A
E
+
∠
E
D
B
)
=
2
∗
4
5
°
=
9
0
°
. Then,
∠
A
G
D
=
9
0
°
, so
G
is on the circumference of diameter
A
D
. Since
E
is the incenter of
△
A
G
D
, then
G
E
is the angle bisector of
∠
A
G
D
, but since
P
is the midpoint of the semiarc
A
D
⌢
, then
G
P
is also the angle bisector of
∠
A
G
D
, so
G
,
E
and
P
are collinear. We know that
∠
P
A
O
=
4
5
°
, since
A
O
=
P
O
and
∠
A
O
P
=
9
0
°
, then
∠
A
E
P
=
∠
E
A
G
+
∠
A
G
E
=
∠
E
A
G
+
4
5
°
=
∠
D
A
E
+
4
5
°
=
∠
D
A
E
+
∠
P
A
D
=
∠
P
A
E
. Then,
P
A
=
P
E
=
P
D
, so
P
E
=
P
A
=
A
O
2
+
P
O
2
=
3
3
2
+
3
3
2
=
4
6
.
6
6
9
.
Please fix the latex to make your solution more presentable. Good observation on the harmonic division!
Log in to reply
Thank you! It was my first time using LaTeX, so I did not notice it. Now, it looks so much better!
Using geometry the solution is as under.
 Please enlarge the sketch.
O
1
,
O
2
,
O
3
are the centers of circles on diameters 11, 60 and 66.
G is the point of intersection of EF and AD.
Applying Cos Rule to
△
O
1
O
2
E
,
C
o
s
O
1
O
2
E
=
2
∗
3
0
.
5
∗
3
0
(
3
6
−
5
.
5
)
2
+
3
0
2
−
5
.
5
2
=
.
9
8
3
6
∴
S
i
n
O
1
O
2
E
=
.
0
.
1
8
0
3
I
n
r
t
.
∠
e
d
Δ
E
G
O
2
,
E
G
=
3
0
∗
S
i
n
O
1
O
2
E
=
5
.
4
.
G
O
2
=
3
0
∗
C
o
s
O
1
O
2
E
.
=
2
9
.
5
1
.
P
E
=
G
O
3
2
+
(
P
O
3
+
G
E
)
2
=
(
2
9
.
5
1
−
3
)
2
+
3
8
.
4
2
=
4
6
.
6
6
9
.
Please enlarge the sketch.
O
1
,
O
2
,
O
3
are the centers of circles on diameters 11, 60 and 66.
G is the point of intersection of EF and AD.
Applying Cos Rule to
△
O
1
O
2
E
,
C
o
s
O
1
O
2
E
=
2
∗
3
0
.
5
∗
3
0
(
3
6
−
5
.
5
)
2
+
3
0
2
−
5
.
5
2
=
.
9
8
3
6
∴
S
i
n
O
1
O
2
E
=
.
0
.
1
8
0
3
I
n
r
t
.
∠
e
d
Δ
E
G
O
2
,
E
G
=
3
0
∗
S
i
n
O
1
O
2
E
=
5
.
4
.
G
O
2
=
3
0
∗
C
o
s
O
1
O
2
E
.
=
2
9
.
5
1
.
P
E
=
G
O
3
2
+
(
P
O
3
+
G
E
)
2
=
(
2
9
.
5
1
−
3
)
2
+
3
8
.
4
2
=
4
6
.
6
6
9
.
If you let A:(0,0), B:(6,0),C:(11,0) & D: (66,0) then we may obtain E as intersection of (x-11/2)²+y²=(11/2)² and (x-36)²+y²=(30)² which turns out to be (396/61,330/61) while P is (33,-33). From which we can determine PE as 33√2 or ~ 46.669
Aah ! It hurts. Just a minor calculation mistake .:(
Using the analytical approach for this problem is very natural. Great job.