SAT Functions
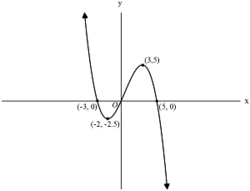The function
is shown above. What are all the values of
for which
is negative?
(A)
(B)
(C)
(D)
(E)
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Correct Answer: C
Solution 1:
The negative values of f ( x ) are shown below in the shaded region.
As can be seen, the x − values for which f ( x ) is negative are − 3 < x < 0 and 5 < x < ∞ .
Solution 2:
Tip: Look for a counter-example.
(A) If x = 3 , then f ( 3 ) = 5 > 0 . Wrong choice.
(B) If x = − 3 , then f ( − 3 ) = 0 , which isn't less than 0 . Wrong choice.
(D) If x = 6 , f ( x ) will be located below the x − axis, and therefore will be negative. So, choice (D) is only half of the solution. Eliminate this choice.
(E) If x = 3 , then f ( 3 ) = 5 > 0 . Wrong choice.
We couldn't find a counter-example for choice (C). Therefore it is the correct answer.
Incorrect Choices:
(A) , (B) , (D) , and (E)
Solution 2 finds a counter-example for each of these wrong choices.