SAT Geometry Student-Produced Response
Level
1
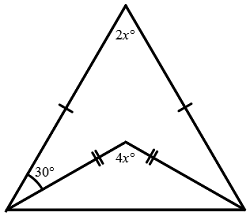 If the two triangles shown above are isosceles, what is the value of
If the two triangles shown above are isosceles, what is the value of
The answer is 30.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Correct Answer: 30
Solution:
Refer to the diagram below.
Because the bigger triangle is isosceles, 2 y + 2 x = 1 8 0 and y = 2 1 8 0 − 2 x = 9 0 − x .
Likewise, because the smaller triangle is isosceles, 4 x + 2 z = 1 8 0 , or z = 2 1 8 0 − 4 x = 9 0 − 2 x .
3 0 + z 3 0 + 9 0 − 2 x 1 2 0 − 2 x 3 0 = y = 9 0 − x = 9 0 − x = x
Common Mistakes:
If you got this problem wrong, you should review SAT Triangles .