SAT Lines
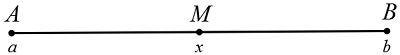 In the diagram above, points
and
have coordinates
and
such that
If
is the midpoint of segment
and
has the coordinate
all of the following are true EXCEPT:
In the diagram above, points
and
have coordinates
and
such that
If
is the midpoint of segment
and
has the coordinate
all of the following are true EXCEPT:
(A)
(B)
(C)
(D)
(E)
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Correct Answer: E
Solution:
Tip: The midpoint of a segment divides it in half.
We show why all of the answer choices are true, except choice (E):
(A) If M is the midpoint of segment A B , then A M = M B = 2 1 A B . Therefore this statement is true.
(B) Recall that if m and n are on a number line, and m < n , then the distance between m and n is n − m . In this case, b > x and therefore M B = b − x . This statement is true.
(C) By definition, the midpoint divides a segment into two congruent segments. If M is the midpoint of A B , as is the case here, then A M ≅ M B .
(D) A M = a − x and B M = b − x . By the definition of a midpoint, A M ≅ M B or A M = M B . It follows then that a − x = b − x , and re-arranging, we obtain 2 x = a + b . Therefore (D) is also true.
(E) Following the reasoning in (D), we conclude that x = 2 a + b = 2 b − a . Option (E) is false, and it is the correct answer.
Incorrect Choices:
(A) , (B) , (C) , and (D)
The solution explains why these choices are wrong.