SAT Math IX
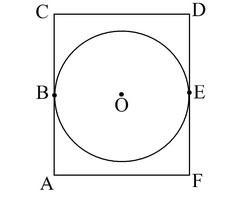 In the figure above,
A
C
D
F
is a rectangle and the circle with center
O
has a radius of
r
.
A
C
is tangent to the circle at point
B
,
D
F
is tangent to the circle at point
E
, and
∠
C
O
E
measures
1
2
0
°
. If
C
F
(not shown) passes through
O
, then what is the length of
C
F
in terms of
r
?
In the figure above,
A
C
D
F
is a rectangle and the circle with center
O
has a radius of
r
.
A
C
is tangent to the circle at point
B
,
D
F
is tangent to the circle at point
E
, and
∠
C
O
E
measures
1
2
0
°
. If
C
F
(not shown) passes through
O
, then what is the length of
C
F
in terms of
r
?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
Sin30=r/co , co=2r cf=2co then cf=4r
ACDF is rectangle, therefore ∠A, ∠C, ∠D & ∠F is 90 degree ∠COE=120 & ∠OEF= 90 Therefore ∠EOF= 180-120=60 and ∠OFE= 30 degree As, AC||DF and Line CF passes through center O, therefore CO=OF
ΔOEF has three angle of 90, 60 & 30. And OE= r Sin ∠OFE=OE/OF = r/OF OF= r/ Sin30= 2r As OF=CO, Therefore, CF= 2* OF= 4r
The phrase in terms of means that this is a Plugging In question. The figure above the question is not drawn to scale, so redraw or add to the figure based on information in the question.
Because A C and D F are tangent to the circle, they form a 9 0 ° angle with a radius or diameter of the circle. Draw in diameter B E and mark the right angles. Draw the diagonal of the rectangle C F . The question states that ∠ C O E = 1 2 0 ° so ∠ C O B = 6 0 ° . We have a 30-60-90 triangle, C O B , in which O B is the radius of the circle and the shortest side of the triangle.
Time to Plug In! If r = 5 , the sides of this special right triangle are 5 : 5 3 : 1 0 . So C O = 1 0 , which is half the length of C F , which must be equal 20. Now Plug In r = 5 in the answers:
A results in 1 0 3 ;
B gives 2 0 ;
C gives 2 0 π ;
D gives 1 0 2 .
Only B has a result of 2 0 .
Solution credit: The Princeton Review
in quadrilateral COED angle CDE =90 , angle OED=90 & angle given that angle COE=120 . thus applying angle sum rule angle OCD=360-120-90-90=60 . now in triangle CFD CD=2R & by angle sum property of triangle angle CFD= 180-90-60=30 . now sin30=2R/CF, so CF=2R/Sin30=2R*2=4R
Angle COE = 120, so angle COB is 60. Using trigonometry where cos COB = BO/CO. Thus, cos 60 = r/CO <=> CO = 2r. CO = OF, hence CF = CO+OF. CF = CO + CO = 2CO = 2(2r) = 4r
∆OCB, <COB=60⁰ (<BOE-<COE => 180⁰-120⁰) Cos60⁰=OB/OC OC=OB/0.5=2r (Cos60⁰=1/2; OB=r) CF=2OC=4r
Let the midpoint of C D be M . Note that since ∠ M O E = 9 0 and ∠ C O E = 1 2 0 , we have ∠ C O M = 3 0 and ∠ B O C = 6 0 , and thus ∠ O F E = 6 0 as well. Now, let the radius be r . By 3 0 − 6 0 − 9 0 triangles, we have C O = F O = 2 r → C F = 2 r + 2 r = 4 r .
Yes that is a simple and bright solution,Thanks. K.K.GARG,India
You should say ANGLE COE measures 120 DEGREES
Thanks, Michael. I got this from my SAT book, which doesn't specify, but I'll fix it to that because it's more clear this way.
BO/CO = cos(180-120) = 0.5 CO = 2 * BO = 2*R CF = 2 * CO = 2 * 2 * R = 4R