Parallel Lines
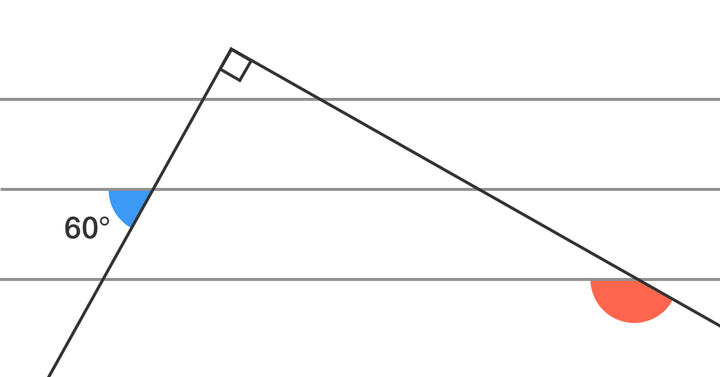
Given that all three of the horizontal lines are parallel, what is the measurement of the red angle in degrees?
Note : The diagram is not drawn to scale.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Discussions for this problem are now closed
AHh I was so used to the right angle. I was thinking the answer was 120 x'D so i was like maybe 135 LOL
i don't know why it deceived me to think that the top triangle have a 90 - 60 - 60 angles :D :D
thank you so much.
Solution 1:
Tip: Know the Properties of Parallel Lines.
Tip: An exterior angle in a triangle equals the sum of the two nonadjacent interior angles.
Refer to the diagram below.
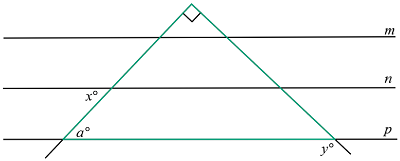
x and a are alternate interior angles. Therefore x = a . The two transversals and line p form a triangle, shown in the figure in green. We know that in a triangle, the measure of an exterior angle equals the sum of the measures of the two nonadjacent interior angles. Therefore, y = a + 9 0 = x + 9 0 , which is choice (B).
Solution 2:
Tip: Know the Properties of Parallel Lines.
Tip: The two acute angles in a right triangle are complementary.
Refer to the diagram below.
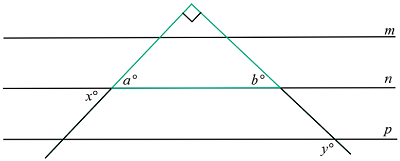
x and a are vertical angles. Therefore x = a .
a and b are the acute angles in a right triangle, shown in green, and therefore add to 9 0 ∘ . It follows that b = 9 0 − a .
y and b are same-side exterior angles. Same-side exterior angles are supplementary and therefore y + b = 1 8 0 . We solve this equation:
y + b y y \ y y y = = = = = = 1 8 0 1 8 0 − b 1 8 0 − ( 9 0 − a ) 1 8 0 − 9 0 + a 9 0 + a 9 0 + x same-side exterior angles are supplementary substitute b = 9 0 − a
Right, but the image is wrong. It suggests the idea that the triangle is isosceles. In that case, the angle you claim to be 60°, would be 45°.
The image is not wrong. It may look like an isosceles triangle but it's not.
The 6 0 ° clearly indicates that it's not an isosceles triangle.
Edit: Whoever downvoted my comment should indicate and explain where I could be wrong at, not just downvoting and running away. You can't learn math this way.
there is a vertically opposite angle = 60 and if we consider the small right triangle we get the third side which is 30, the angle below it is also 30 ( corresponding angles ) now we know that a straight line = 180 degrees therefore 30+ red angle = 180 degrees, red angle = 150 degrees
Relevant wiki: SAT Lines and Angles