SAT Polygons

Geometry Level 2

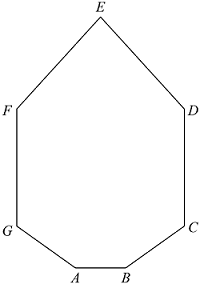
A diagonal in a polygon is defined as a segment connecting two non-adjacent vertices. How many diagonals does the figure above have?

(A) $\ \ 14$
(B) $\ \ 16$
(C) $\ \ 17$
(D) $\ \ 18$
(E) $\ \ 28$

A B C D E

2 solutions

Tatiana Georgieva Staff
Feb 28, 2015

Correct Answer: A

Solution 1:

Tip: Draw a picture.
We draw all of the diagonals and count them, making sure not to repeat or miss any of them. We count 14 diagonals. These are shown below.

Solution 2:

Because sides of the polygon do not count as diagonals, from each vertex we can draw $7-3 = 4$ diagonals. The diagonals for vertex $A$ are shown below.

There are 7 vertices in total. So, there are $7\cdot 4 = 28$ diagonals that can be drawn, four from each vertex.

But, because we are counting each diagonal twice -- $\overline{AF}$ is drawn from vertex $A$ to vertex $F$ and $\overline{FA}$ is drawn from vertex $F$ to vertex $A$ -- we must divide our result by 2.

So, in a heptagon, there are $28:2 = 14$ diagonals.

Incorrect Choices:

(B) , (C) , and (D)
If you miscount, you may get one of these wrong choices.

(E)
If you count each diagonal twice, you will get this wrong answer.

Nice solution. In general, for an $n$ -sided convex polygon the number of diagonals $D_{n}$ will be the number of combinations of $2$ vertices chosen from $n$ vertices, minus the number of sides of the polygon, (as these are not considered as diagonals). Thus

$D_{n} = \dbinom{n}{2} - n = \dfrac{n(n - 1)}{2} - n = \dfrac{n(n - 3)}{2}.$

So in this case $D_{7} = \dfrac{7(7 - 3)}{2} = 14.$

Brian Charlesworth - 6 years, 3 months ago

Lalit Jena
Mar 4, 2015

n*(n-3)/2 where n is side of the polygon So 7(7-3)/2= 14 that'll !! Simple :-)

derivation of that formula comes from combinatorics... Brian has given the whole thing before you!

Sarthak Rath - 6 years, 3 months ago

You are right Mrs. Sarthak!!! Mr. Brian u are great!!! :-)

Lalit Jena - 6 years, 3 months ago

SAT Polygons

2 solutions

0 pending reports