SAT1000 - P329
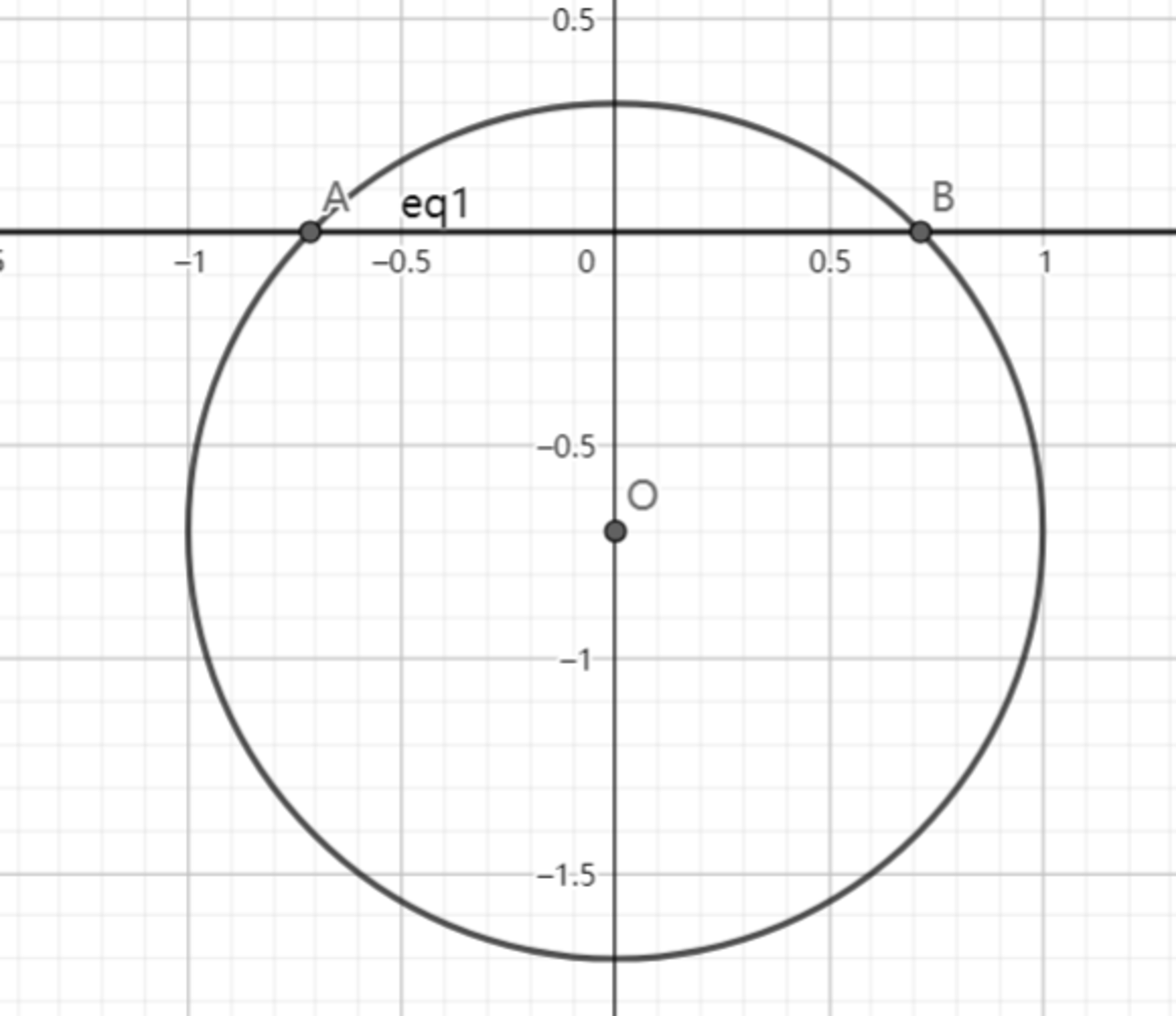
As shown above, the circle has radius , is its center. At , is at , and it is moving at upwards along the y-axis. Let be the length of the arc above the x-axis, .
For , what is the best graph for ?
Have a look at my problem set: SAT 1000 problems
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
At t = 0 , there is no part of the circle above the x -axis. That means x ( 0 ) = 0 and f ( 0 ) = cos ( x ( 0 ) ) = cos ( 0 ) = 1 , so the graph of f ( t ) should go through ( 0 , 1 ) .
At t = 1 , O is at the origin, and exactly half the circle is above the x -axis. That means x ( 1 ) = π and f ( 1 ) = cos ( x ( 1 ) ) = cos ( π ) = − 1 , so the graph of f ( t ) should go through ( 1 , − 1 ) .
When ∠ A O B is a right angle, △ A O B is an isosceles right triangle with a height of 2 2 , and exactly one fourth of the circle is above the x -axis. That means t = 1 − 2 2 ≈ 0 . 2 9 3 , x ( 0 . 2 9 3 ) = 2 π and f ( 0 . 2 9 3 ) = cos ( x ( 0 . 2 9 3 ) ) = cos ( 2 π ) = 0 , so the graph of f ( t ) should go through ( 0 . 2 9 3 , 0 ) .
The only graph that goes through ( 0 , 1 ) , ( 1 , − 1 ) , and ( 0 . 2 9 3 , 0 ) is B .