SAT1000 - P527
Given that a , b ∈ R , a + b = 2 , b > 0 , then find the minimum value of 2 ∣ a ∣ 1 + b ∣ a ∣ .
Let M be the minimum value. Submit ⌊ 1 0 0 0 M ⌋ .
Have a look at my problem set: SAT 1000 problems
The answer is 750.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Case 2: you copied -1 from case 1.
I think we had this conversation before! But, here I go again.
Unwarranted application of AM-GM is almost always bad. f ( x ) ≥ g ( x ) doesn't mean f ( x ) achieves a minimum value when f ( x ) = g ( x ) . For example, why didn't you apply AM-GM for the terms 2 ( 2 − b ) 1 a n d b 2 ? It's because you wouldn't get to the correct answer applying the same logic as you applied here. Graphing 2 ( 2 − b ) 1 + b 2 and 2 b ( 2 − b ) 1 would make the fallacy clear.
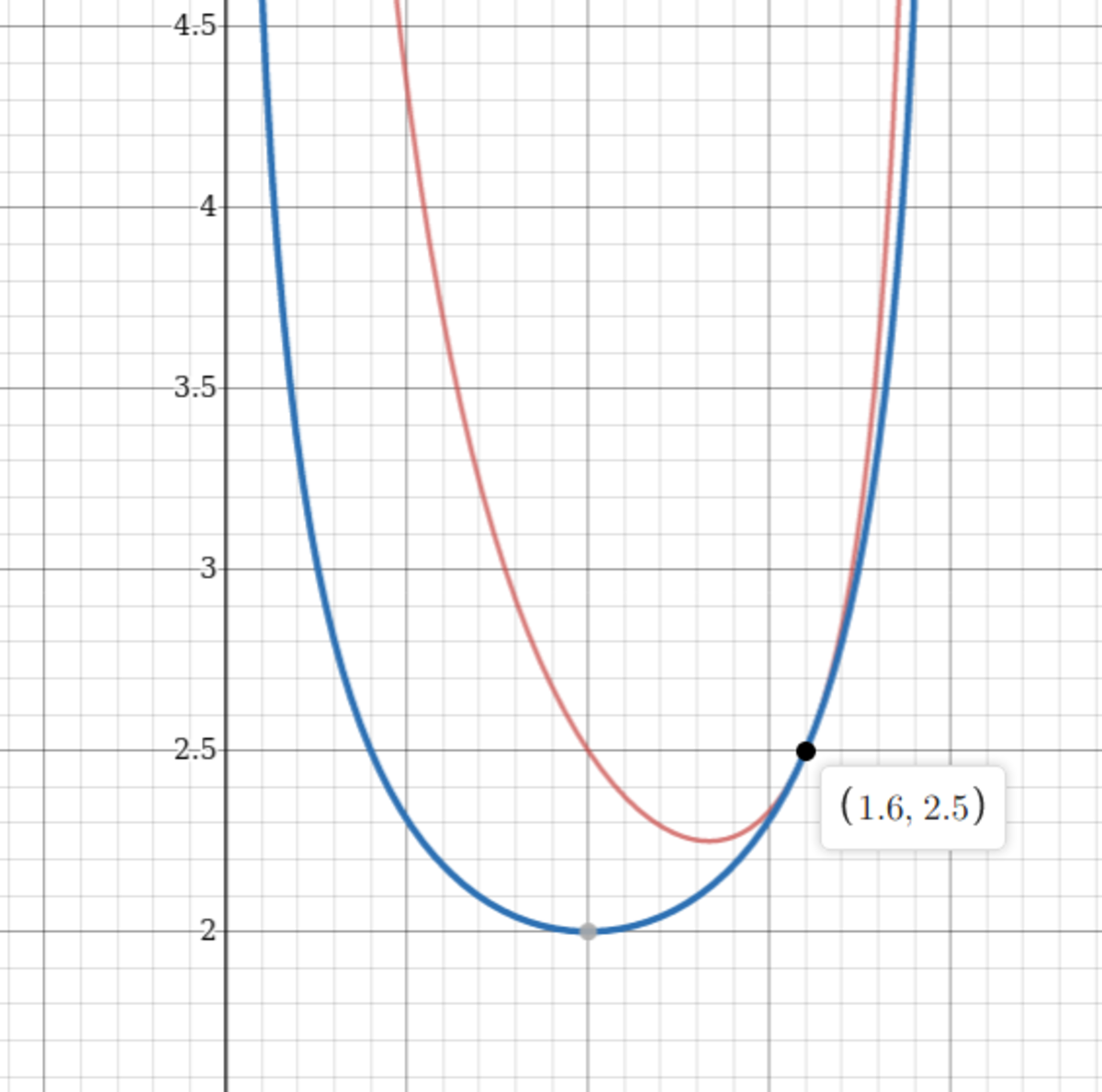 AM-GM Fallacy
AM-GM Fallacy
As long as you can't justify your reasoning for arranging the terms in a certain way to get the proper result, the solution has no logical basis at all!
I will also point at your usage of = sign right after ≥ saying "equality occurs at some point". This is also wrong. You cannot write this mathematically as the functions of b are not 'constant' functions. You have to use f ( b = 4 ) to make use of the = sign.
No worry, thanks again.
This problem can be solved using calculus easily. Firstly, we can turn the expression 2 ∣ a ∣ 1 + b ∣ a ∣ into a single variable function using the condition a + b = 2 . Let f ( b ) = 2 ∣ 2 − b ∣ 1 + b ∣ 2 − b ∣
We now take the derivative of f ( b ) . This results in the piecewise function f ′ ( b ) = ( 4 − 2 b ) 2 2 − b 2 2 if b < 2 and − ( 2 b − 4 ) 2 2 + b 2 2 if b > 2 with a discontinuity at b = 2. Since we are trying to find the minimum of f ( b ) , we must find the critical points of f ( b ) . It just so happens that in both halves this occurs when b 2 = ( 4 − 2 b ) 2 . Rearranging terms yields the quadratic equation 3 b 2 − 1 6 b + 1 6 = 0 which has the roots b = 1 . 3 3 3 , 4 .
Since we are given that there exists a global minimum, one of these critical points must be the global minimum (under different circumstances I would have to show that one of these is a global minimum, most likely via a second-derivative test). Plugging both roots into f ( b ) yields the local minimums (1.333, 1.25) and (4, 0.75). It is clear that M = 0.75 meaning that ⌊ 1 0 0 0 M ⌋ = 7 5 0
Let the given sum be S . Then
l i m a → − ∞ S = 1 , l i m a → 0 − S = ∞
In the range ( − ∞ , 0 ) , it has one minimum at a = − 2 , b = 4 , the minimum value being 0 . 7 5 .
Also, l i m a → 0 + S = l i m a → 2 − S = ∞ .
Since b > 0 , a < 2
In the range [ 0 , ∞ ) , s has one minimum at a = 3 2 , b = 3 4 , the minimum value being 1 . 2 5 > 0 . 7 5 .
Hence the given sum can never be less than 0 . 7 5 .
Shouldn’t the limit of given sum when a is approaching to positive or negative infinity be 1?
2 ∣ a ∣ 1 + b ∣ a ∣ = 2 ∣ 2 − b ∣ 1 + b ∣ 2 − b ∣ = ⎩ ⎪ ⎨ ⎪ ⎧ 2 ( 2 − b ) 1 + b 2 − b 2 ( b − 2 ) 1 + b b − 2 for 0 < b ≤ 2 for b > 2
Case 1: 0 < b ≤ 2
f ( b ) f ′ ( b ) min ( f ( b ) ) = 2 ( 2 − b ) 1 + b 2 − b = 2 ( 2 − b ) 2 1 − b 2 2 = − 2 ( 2 − b ) 2 b 2 3 b 2 − 1 6 b + 1 6 = − 2 ( 2 − b ) 2 b 2 ( 3 b − 4 ) ( b − 4 ) = f ( 3 4 ) = 4 5
Case 2: b > 2
f ( b ) f ′ ( b ) min ( f ( b ) ) = 2 ( b − 2 ) 1 + b b − 2 = − 2 ( b − 2 ) 2 1 + b 2 2 = 2 ( 2 − b ) 2 b 2 ( 3 b − 4 ) ( b − 4 ) = f ( 4 ) = 4 3
Therefore the minimum value M = 4 3 = 0 . 7 5 , ⟹ ⌊ 1 0 0 0 M ⌋ = 7 5 0 .