SAT1000 - P594

Geometry Level 3

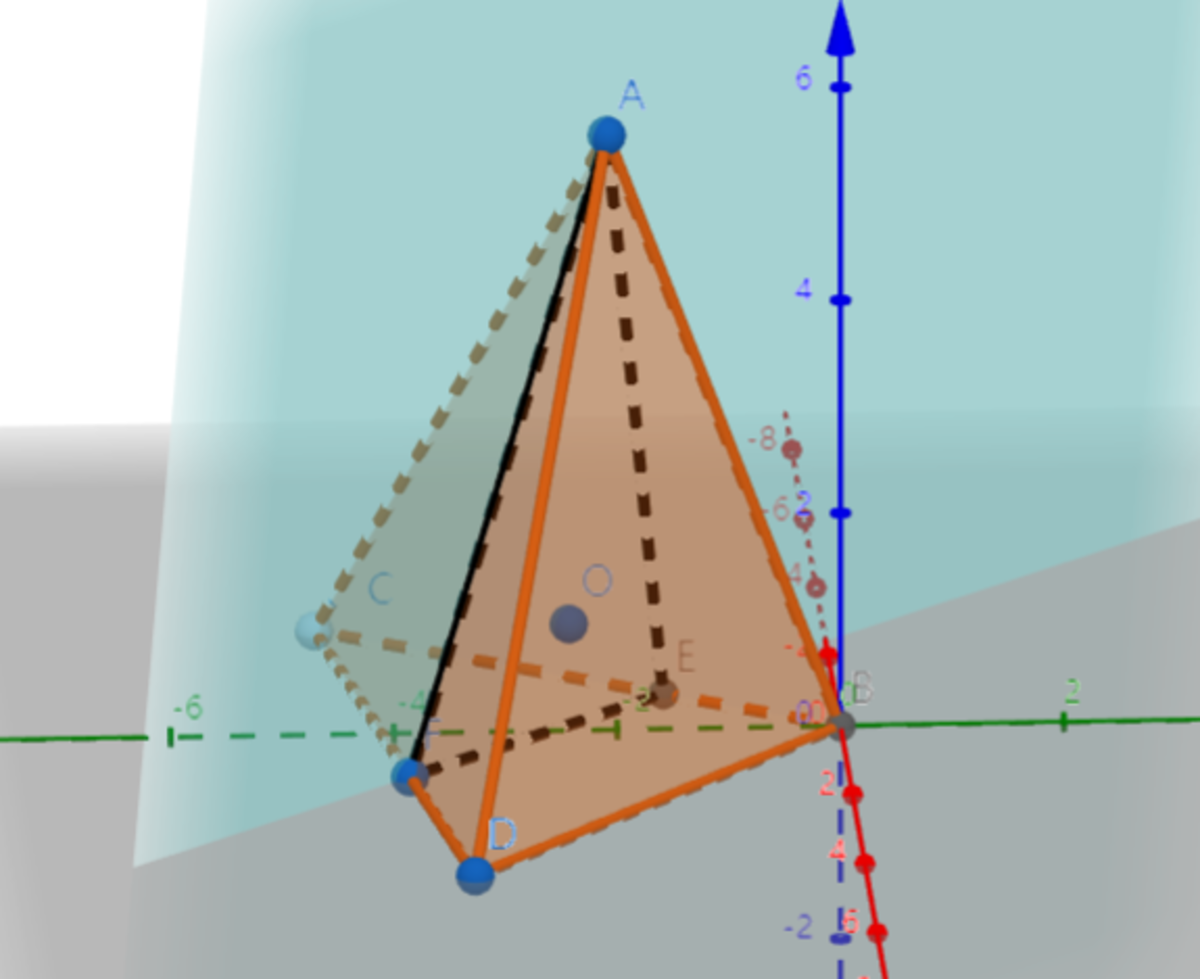
As shown above, in triangular pyramid $A-BCD$ , the cross section $AEF$ passes through the center of the inscribed sphere $O$ (i.e. The sphere which is tangent to all of the faces of the solid) of $A-BCD$ , and it intersects with $BC, DC$ at point $E,F$ respectively.

If the cross section divides the pyramid into two parts whose volumes are equal, $S_1$ is the surface area of solid $A-BEFD$ , $S_2$ is the surface area of solid $A-EFC$ , what is always true for $S_1$ and $S_2$ ?

Have a look at my problem set: SAT 1000 problems

S_1<S_2

Can't say.

S_1=S_2

S_1>S_2

1 solution

Hosam Hajjir
Jun 8, 2020

Let's express the volume of the two parts of the triangular pyramid in terms of the areas of their surfaces:

$\text{Volume of A-BEFD} = \frac{1}{3} r ( [ABE] + [AFD] + [ADB]+[BEFD] )$

where $r$ is the radius of the inscribed sphere, and $[\cdot]$ denotes the area of the indicated polygon. Similarly,

$\text{Volume of A-EFC} = \frac{1}{3} r ([AEC] + [AFC] + [EFC] )$

Since the two volumes are equal , we deduce that,

$[ABE] + [AFD] + [ADB]+[BEFD] =[AEC] + [AFC] + [EFC]$

Adding $[AEF]$ to both sides, results in

$S_1 = S_2$

SAT1000 - P594

1 solution

0 pending reports