SAT1000 - P759
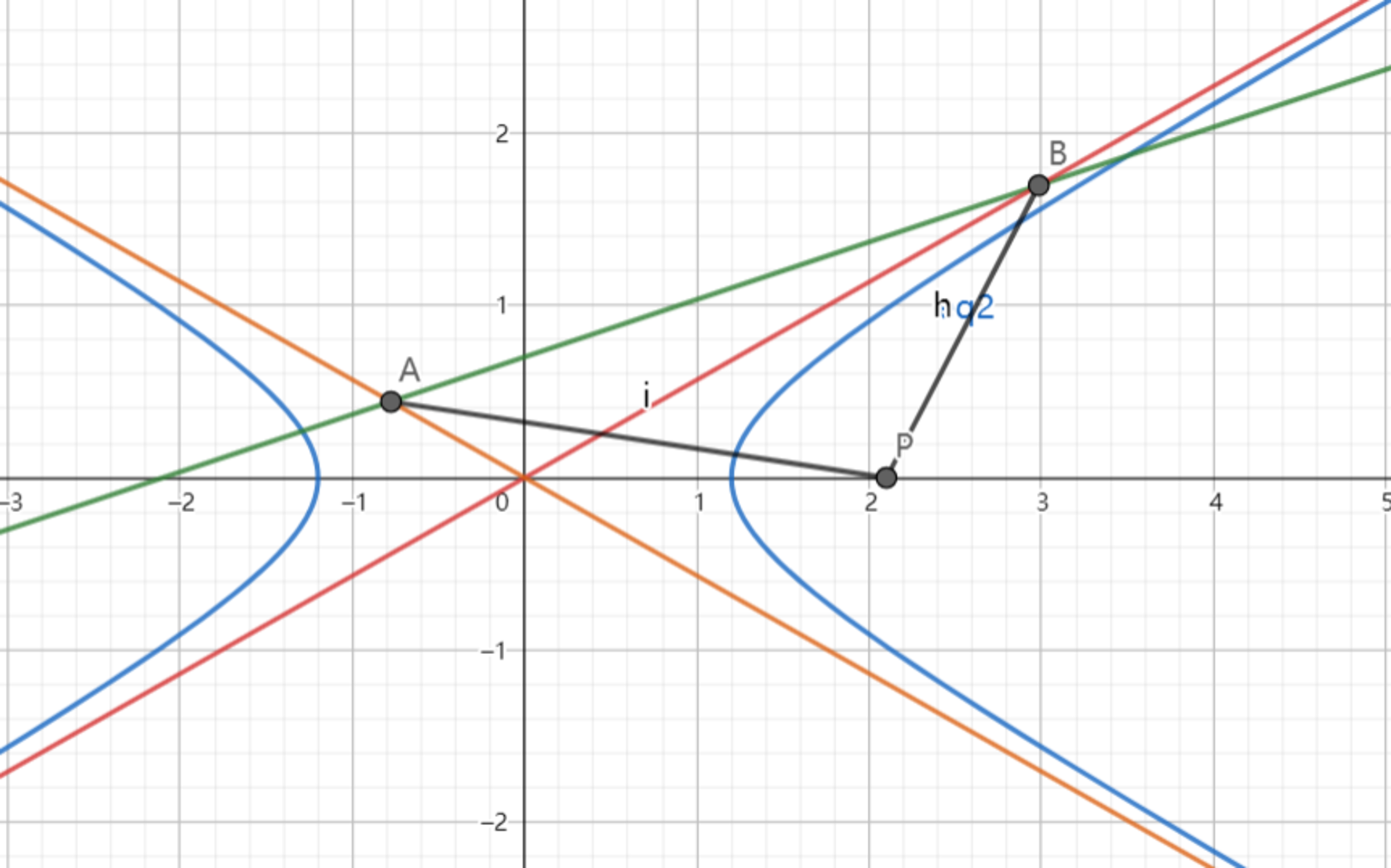
As shown above, the line: intersects with the two asymptotes of the hyperbola:
at point .
If point is at and , find the eccentricity of the hyperbola.
Let denote the eccentricity, submit .
Have a look at my problem set: SAT 1000 problems
The answer is 1118.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Equations of asymptotes of given hyperbola is y = a b x and y = − a b x .
Points A and B can be determined by the intersection of each asymptote with the line: x − 3 y + m = 0 . We get
A = ( 3 b + a − m a , 3 b + a m b ) B = ( 3 b − a m a , 3 b + a m b )
Point P is at ( m , 0 ) .
P A 2 = ( m − 3 b + a − m a ) 2 + ( 0 − 3 b + a m b ) 2
⇒ P A 2 = m 2 + ( 3 b + a ) 2 m 2 a 2 + 3 b + a 2 m 2 a + ( 3 b + a ) 2 m 2 b 2
⇒ P A 2 = m 2 ( ( 3 b + a ) 2 ( 3 b + a ) 2 + a 2 + 2 a ( 3 b + a ) + b 2 )
⇒ P A 2 = ( 3 b + a ) 2 m 2 ( 4 a 2 + 1 0 b 2 + 1 2 a b ) ⋯ Eq. 1
Similarly, writing for P B 2
P B 2 = ( m − 3 b − a m a ) 2 + ( 0 − 3 b − a m b ) 2
⇒ P B 2 = m 2 + ( 3 b − a ) 2 m 2 a 2 − 3 b − a 2 m 2 a + ( 3 b − a ) 2 m 2 b 2
⇒ P B 2 = m 2 ( ( 3 b − a ) 2 ( 3 b − a ) 2 + a 2 − 2 a ( 3 b − a ) + b 2 )
⇒ P B 2 = ( 3 b − a ) 2 m 2 ( 4 a 2 + 1 0 b 2 − 1 2 a b ) ⋯ Eq. 2
It is given that ∣ P A ∣ = ∣ P B ∣
⇒ P A 2 = P B 2
Putting the expressions of P A 2 and P B 2 from Eq. 1 and Eq. 2 in the above equation we get
( 3 b + a ) 2 m 2 ( 4 a 2 + 1 0 b 2 + 1 2 a b ) = ( 3 b − a ) 2 m 2 ( 4 a 2 + 1 0 b 2 − 1 2 a b )
⇒ ( 3 b + a ) 2 2 a 2 + 5 b 2 + 6 a b = ( 3 b − a ) 2 2 a 2 + 5 b 2 − 6 a b
⇒ 2 a 2 + 5 b 2 + 6 a b ( 3 b + a ) 2 = 2 a 2 + 5 b 2 − 6 a b ( 3 b − a ) 2 [ Reciprocating both sides ]
⇒ 2 a 2 + 5 b 2 + 6 a b a 2 + 9 b 2 + 6 a b = 2 a 2 + 5 b 2 − 6 a b a 2 + 9 b 2 − 6 a b
⇒ 1 + 2 a 2 + 5 b 2 + 6 a b 4 b 2 − a 2 = 1 + 2 a 2 + 5 b 2 − 6 a b 4 b 2 − a 2
⇒ 2 a 2 + 5 b 2 + 6 a b 4 b 2 − a 2 = 2 a 2 + 5 b 2 − 6 a b 4 b 2 − a 2
Above equation is true only if numerator is 0 or denominators are equal. Denominator can be equal when any one of a or b is 0 which is not possible for existence of hyperbola. So numerator must be 0 .
⇒ 4 b 2 − a 2 = 0
⇒ b 2 a 2 = 4 ⇒ a 2 b 2 = 4 1
Eccentricity of hyperbola is given by E = 1 + a 2 b 2
So, E = 1 + 4 1 = 4 5 = 2 5
⇒ 1 0 0 0 E = 1 0 0 0 2 5 = 5 0 0 5 ≈ 1 1 1 8 . 0 3 4
⇒ ⌊ 1 0 0 0 E ⌋ = 1 1 1 8