SAT1000 - P765

Geometry Level pending

Let $A,B$ be the end points of the major axis of the ellipse $C:\dfrac{x^2}{3}+\dfrac{y^2}{m}=1$ .

If there exists point $M$ on the ellipse so that $\angle AMB = \dfrac{2\pi}{3}$ , find the range of $m$ .

These pictures show the two cases:

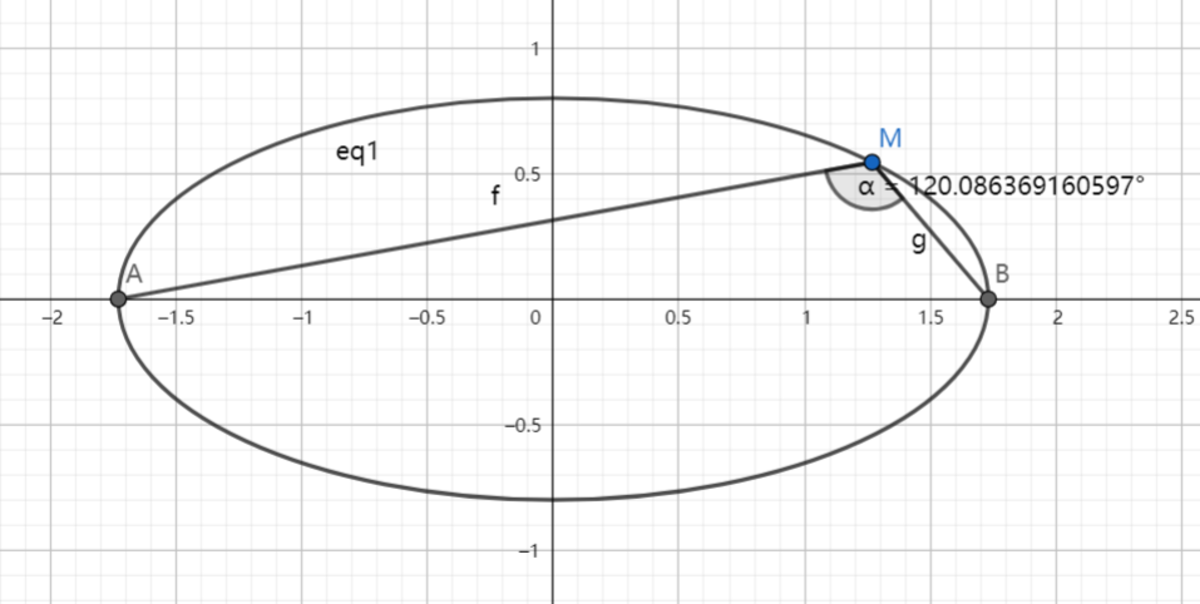
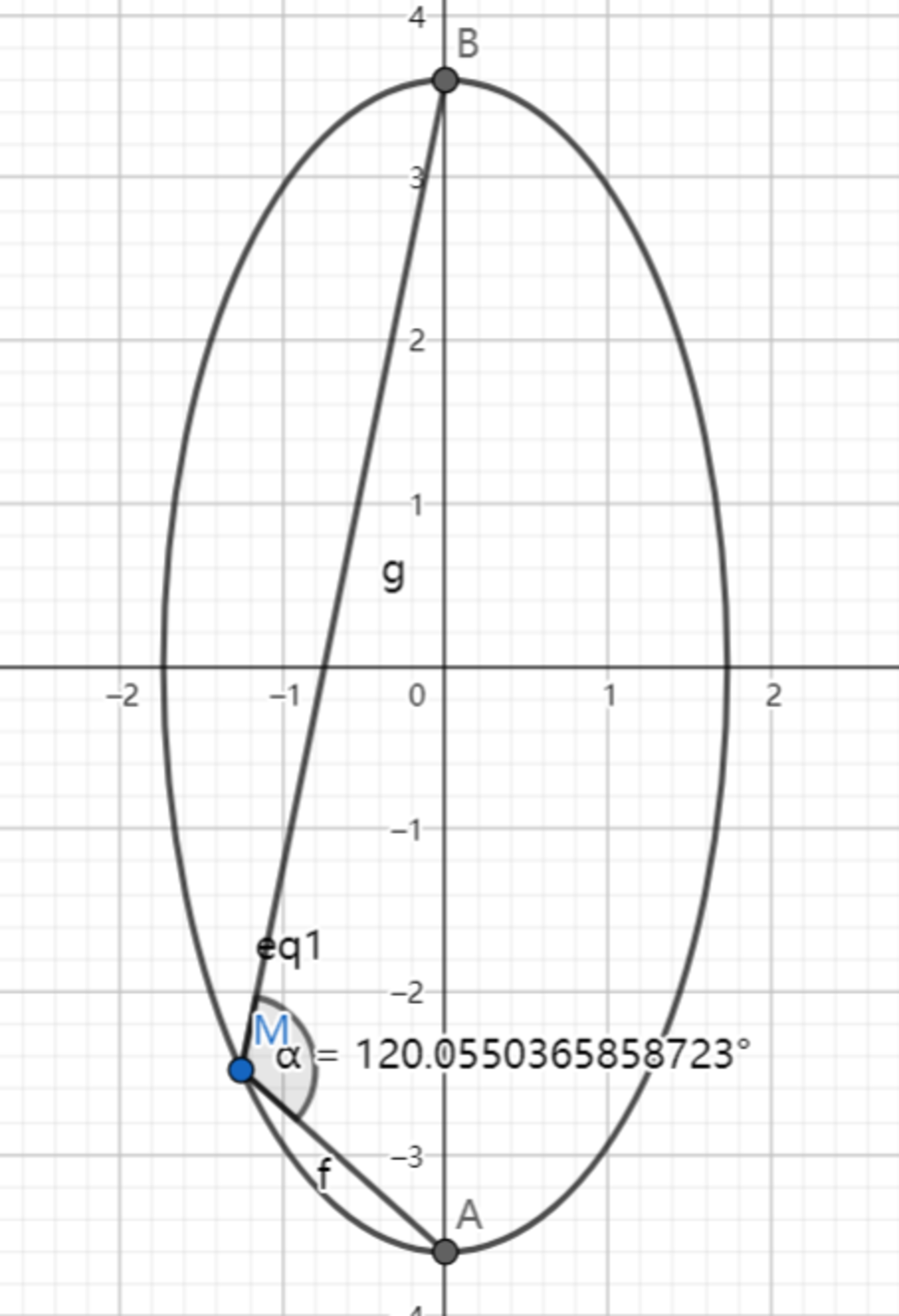
Have a look at my problem set: SAT 1000 problems

(0,1] \cup [9,+\infty)

(0,\sqrt{3}] \cup [9,+\infty)

(0,1] \cup [4,+\infty)

(0,\sqrt{3}] \cup [4,+\infty)

1 solution

A Former Brilliant Member
Jun 8, 2020

Another problem within my reach! Let the position coordinates of $M$ be $(\sqrt 3\cos α,\sqrt m\sin α)$ . (We must have $m> 0$ ). Then

$\tan (\frac{2π}{3})=-\sqrt 3=\dfrac{-\sqrt {\frac{m}{3}}\left (\cot (\frac{α}{2})+\tan (\frac{α}{2})\right )}{1-\frac{m}{3}}$

$\implies \dfrac{3-m}{\sqrt m}=\cot (\frac{α}{2})+\tan (\frac{α}{2})\geq 2$

$\implies m^2-10m+9\geq 0\implies m\leq 1$ and $m\geq 9$ .

Hence the range of $m$ is $(0,1]\cup [9,+\infty)$ .