SAT1000 - P766

Geometry Level pending

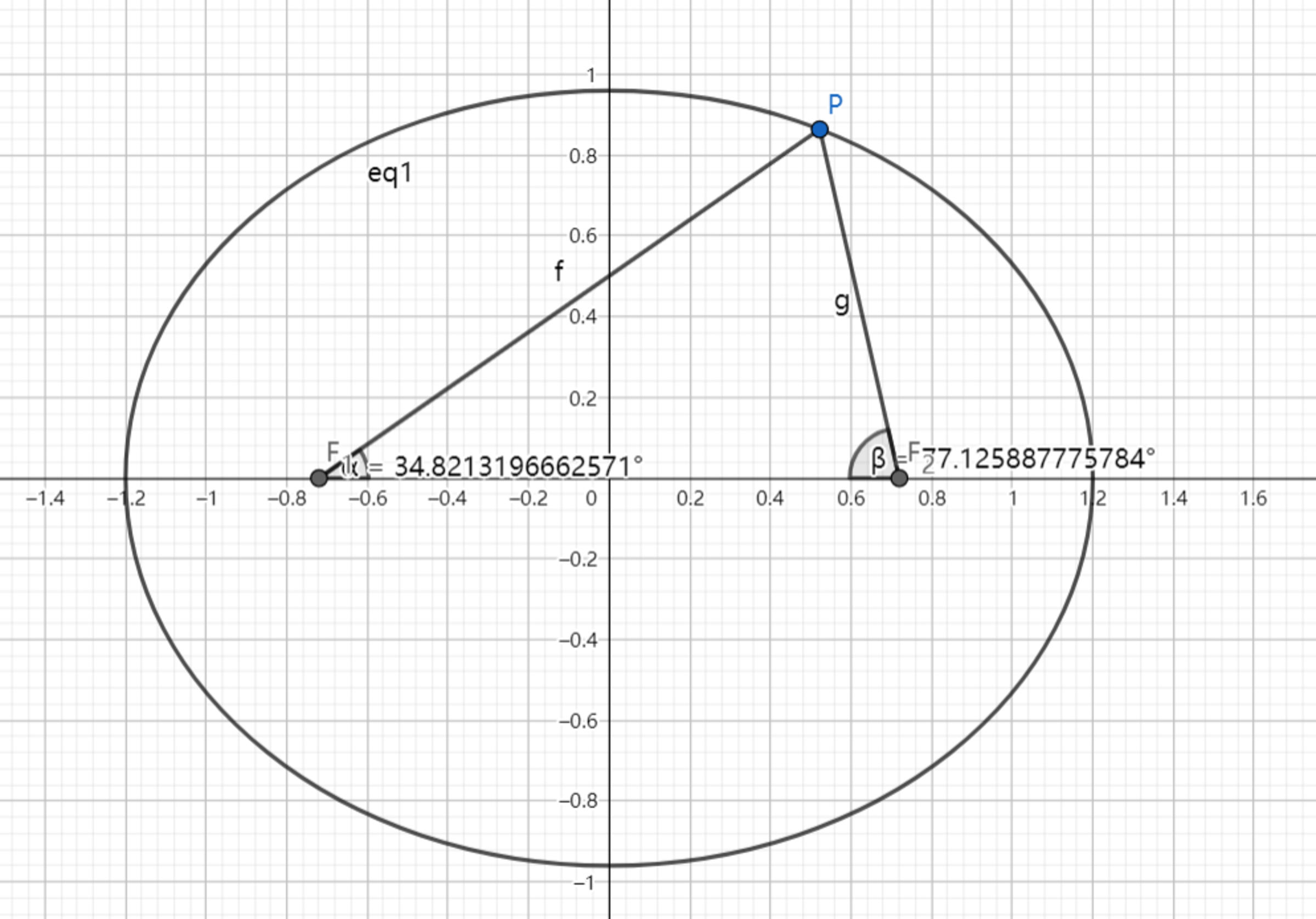
As shown above, the left and right focus of the ellipse: $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1 (a>b>0)$ are $F_1(-c,0), F_2(c,0)$ .

If there exists point $P$ such that $\dfrac{a}{\sin \angle PF_1F_2}=\dfrac{c}{\sin \angle PF_2F_1}$ , find the range of the eccentricity of the ellipse.

The range can be expressed as $(l,r)$ . Submit $\lfloor 1000(2r-l) \rfloor$ .

Have a look at my problem set: SAT 1000 problems

The answer is 1585.

1 solution

A Former Brilliant Member
Jun 9, 2020

As shown in the diagram, $|\overline {F_1P}|=f, |\overline {F_2P}|=g$ .

So $f+g=2a\implies f=2a-g$ .

$\dfrac{\sin α}{\sin β}=\dfrac{g}{f}=\dfrac{a}{c}=\dfrac{a}{\sqrt {a^2-b^2}}=\dfrac{1}{E}$ , where $E$ is the required eccentricity.

Therefore $E=\dfrac{2a}{g}-1$ .

Now, $a(1-E)\leq g\leq a(1+E)$

$\implies \dfrac{1+E}{1-E}\geq E\geq \dfrac{1-E}{1+E}\implies E^2+2E-1\geq 0$

$\implies E\geq \sqrt 2 -1$ . Obviously, $E\leq 1$ . So $l=\sqrt 2 -1,r=1\implies 2r-l=2-\sqrt 2 +1=3-\sqrt 2$ .

Hence $\lfloor 1000(2r-l)\rfloor =\boxed {1585}$ .

SAT1000 - P766

The answer is 1585.

1 solution

0 pending reports