SAT1000 - P787
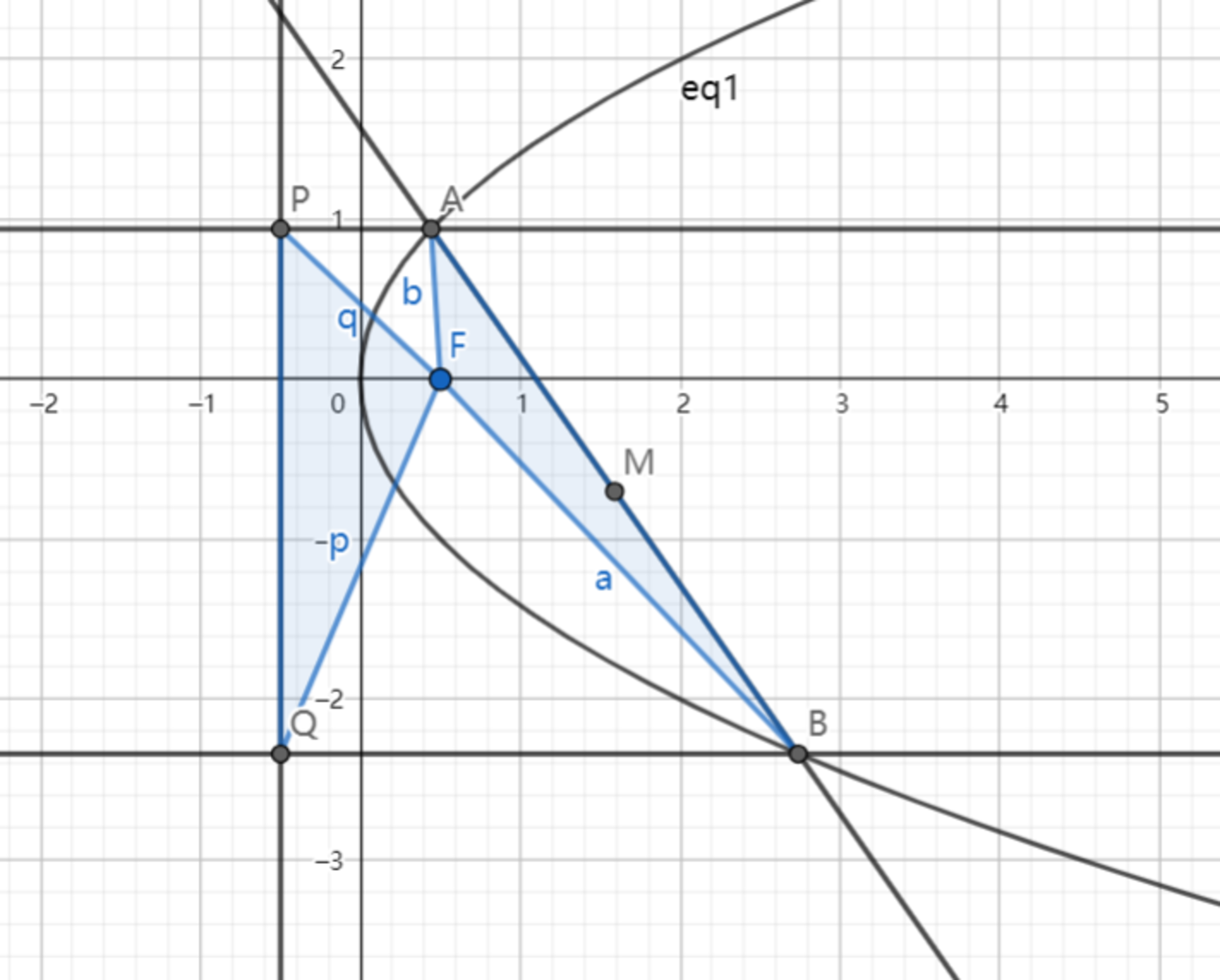
As shown above, the focus of the parabola is . Two lines which are parallel to the x-axis intersect with at and intersect with the directix at . is the midpoint of .
If , find the locus of point .
If the locus can be expressed as , then when , submit the sum of all possible value(s) for .
Note: denotes the area of .
Have a look at my problem set: SAT 1000 problems
The answer is 2501.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The parabola y 2 = 2 x has a focus of F ( 2 1 , 0 ) , so F x = − 2 1 and F y = 0 , and a directrix of x = − 2 1 , so P x = Q x = − 2 1 .
Let p = P y = A y and q = − Q y = − B y . Since A and B are on the parabola y 2 = 2 x , A x = 2 1 p 2 and B x = 2 1 q 2 .
The area of △ P Q F is A △ P Q F = 2 1 ( p + q ) . The area of △ A B F is the area of trapezoid P Q B A minus the sum of A △ P A F , A △ P Q F , and A △ B Q F ; or A △ A B F = 2 1 ( 2 1 ( p 2 + 1 ) + 2 1 ( q 2 + 1 ) ) ( p + q ) − ( 2 1 ( p + q ) + 2 1 ( 2 1 ( p 2 + 1 ) ) p ) + 2 1 ( 2 1 ( q 2 + 1 ) ) q ) . Equating A △ P Q F = 2 A △ A B F and simplifying solves to q = p 2 .
Substituting q = p 2 into B x and B y gives B ( p 2 2 , − p 2 ) .
The midpoint M of A and B is then M = ( 2 1 ( A x + B x ) , 2 1 ( A y + B y ) ) = ( 4 p 2 p 4 + 4 , 2 p p 2 − 2 ) , so the locus of point M is x = 4 p 2 p 4 + 4 and y = 2 p p 2 − 2 . Rearranging these two equations to eliminate p gives f ( x , y ) = y 2 − x + 1 = 0 .
When y = 5 0 , the only possible value for x is x = y 2 + 1 = 5 0 2 + 1 = 2 5 0 1 .