SAT1000 - P802
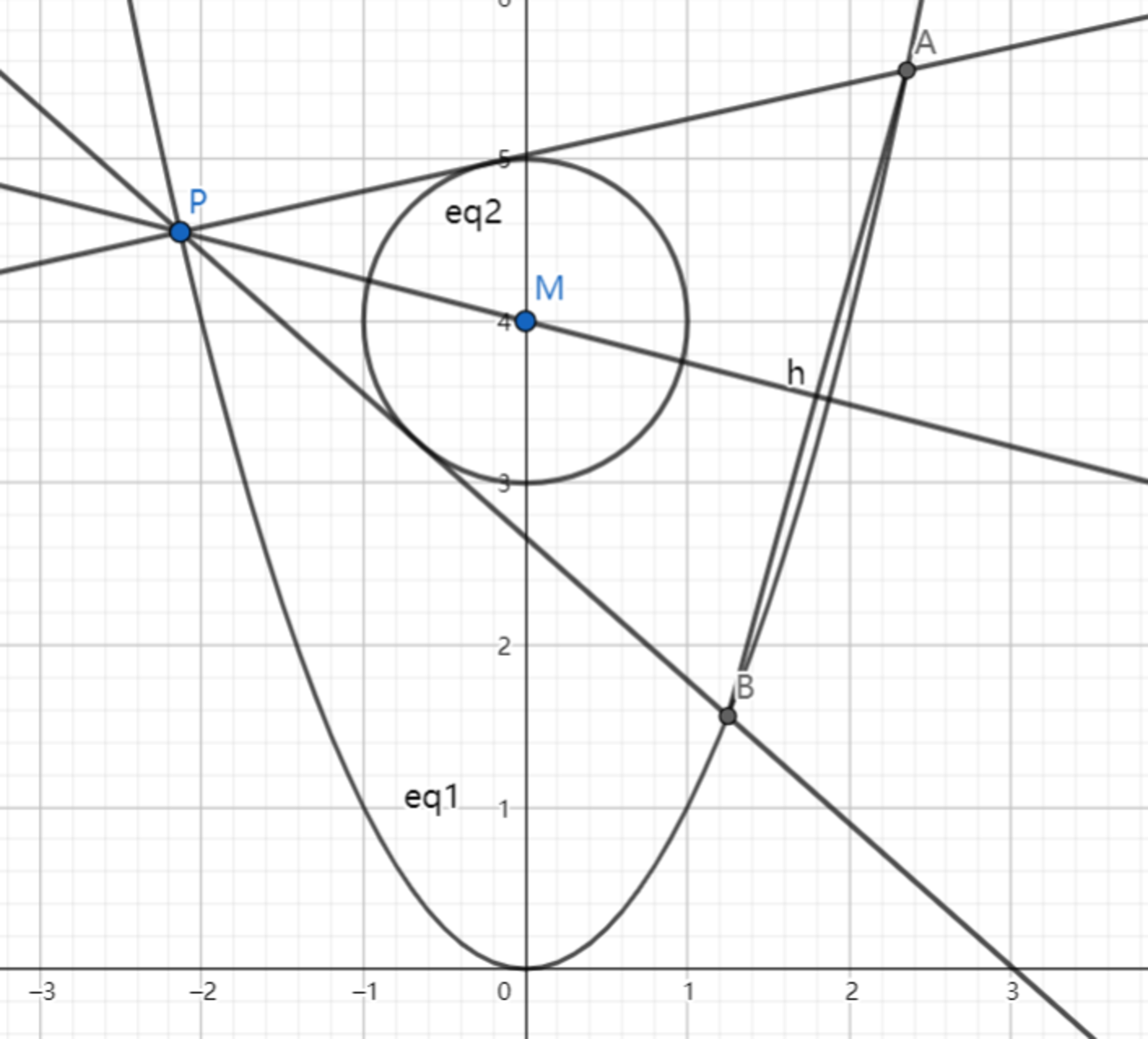
As shown above, the parabola C 1 : x 2 = y , circle C 2 : x 2 + ( y − 4 ) 2 = 1 , and M is the center of circle C 2 .
Point P is a point on C 1 (not at ( 0 , 0 ) ), and l 1 , l 2 are two lines tangent to C 2 and they intersects with C 1 at point A , B respectively. Line l passes through M and P .
If l ⊥ A B , find the equation of line l .
The equation can be expressed as: y = ± k x + b ( k > 0 ) . Submit ⌊ 1 0 0 0 ( k + b ) ⌋ .
Have a look at my problem set: SAT 1000 problems
The answer is 4279.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let the position coordinates of P be ( t , t 2 ) . Then the slopes m 1 , m 2 of the tangents to the circle from P are
t 2 − 1 t ( t 2 − 4 ) ± t 4 − 7 t 2 + 1 5
Points A , B will have position coordinates ( m 1 − t , ( m 1 − t ) 2 ) and ( m 2 − t , ( m 2 − t ) 2 ) .
Let the mid point of A B be D ( 2 m 1 + m 2 − 2 t , 2 ( m 1 − t ) 2 + ( m 2 − t ) 2 ) .
Then t 2 − ( t 2 − 1 ) 2 t 4 + 2 t 2 + 1 5 = 6 t t ( t 2 − 1 ) + 2 1 ⟹ 5 t 6 − 1 8 t 4 − 3 t 2 − 9 2 = 0 .
There are two real solutions to this equation : t ≈ ± 2 . 1 4 5 .
Hence the equation of P D is
y = 6 t t 2 − 1 x + ( t 2 − 1 ) 2 t 4 + 2 t 2 + 1 5 + 2 1 = 4 ± 0 . 2 7 9 7 x .
So, k = 4 , b = 0 . 2 7 9 7 , k + b = 4 . 2 7 9 7 and ⌊ 1 0 0 0 ( k + b ) ⌋ = 4 7 2 9 .
Let D be the point of tangency to the circle on A P , and E be the point of tangency to the circle on B P .
Since P is on the parabola x 2 = y , let its coordinates be P ( p , p 2 ) . Since M is the center of circle x 2 + ( y − 4 ) 2 = 1 , its coordinates are M ( 0 , 4 ) and the radius is D M = E M = 1 .
The slope of M P is then m M P = p p 2 − 4 , and the distance M P is d = p 2 + ( p 2 − 4 ) 2 = p 4 − 7 p 2 + 1 6 .
By the Pythagorean Theorem on △ D M P , D P = M P 2 − D M 2 = ( p 4 − 7 p 2 + 1 6 ) 2 + 1 2 = p 4 − 7 p 2 + 1 5 . Let θ = ∠ D P M = ∠ E P M . Then tan θ = D P D M = p 4 − 7 p 2 + 1 5 1 .
By the angle between two slopes equation, tan θ = 1 + m A P m M P m A P − m M P and tan θ = 1 + m M P m B P m M P − m B P . Substituting m M P = p p 2 − 4 and tan θ = p 4 − 7 p 2 + 1 5 1 and solving gives m A P = p p 4 − 7 p 2 + 1 5 − ( p 2 − 4 ) ( p 2 − 4 ) p 4 − 7 p 2 + 1 5 + p and m B P = p p 4 − 7 p 2 + 1 5 + ( p 2 − 4 ) ( p 2 − 4 ) p 4 − 7 p 2 + 1 5 − p .
The equation of line A P is y = m A P ( x − p ) + p 2 and the equation of line B P is y = m B P ( x − p ) + p 2 . Both A and B are also on x 2 = y , and these equations solve to A ( p 2 − 1 p 4 − 7 p 2 + 1 5 − 3 p , ( p 2 − 1 ) 2 p 4 + 2 p 2 + 1 5 − 6 p p 4 − 7 p 2 + 1 5 ) and B ( p 2 − 1 p 4 − 7 p 2 + 1 5 + 3 p , ( p 2 − 1 ) 2 p 4 + 2 p 2 + 1 5 + 6 p p 4 − 7 p 2 + 1 5 ) .
The slope of A B is then m A B = B x − A x B y − A y = p 2 − 1 − 6 p . Since M P ⊥ A B , m M P m A B = − 1 or p p 2 − 4 p 2 − 1 − 6 p = − 1 , which solves to p = ± 5 1 1 5 .
That means m M P = p p 2 − 4 = ± 5 1 1 5 ( ± 5 1 1 5 ) 2 − 4 = ± 1 1 5 3 1 1 5 , so that the line l has an equation of y = ± 1 1 5 3 1 1 5 x + 4 , so k = 1 1 5 3 1 1 5 , b = 4 , and ⌊ 1 0 0 0 ( k + b ) ⌋ = 4 2 7 9 .