SAT1000 - P839
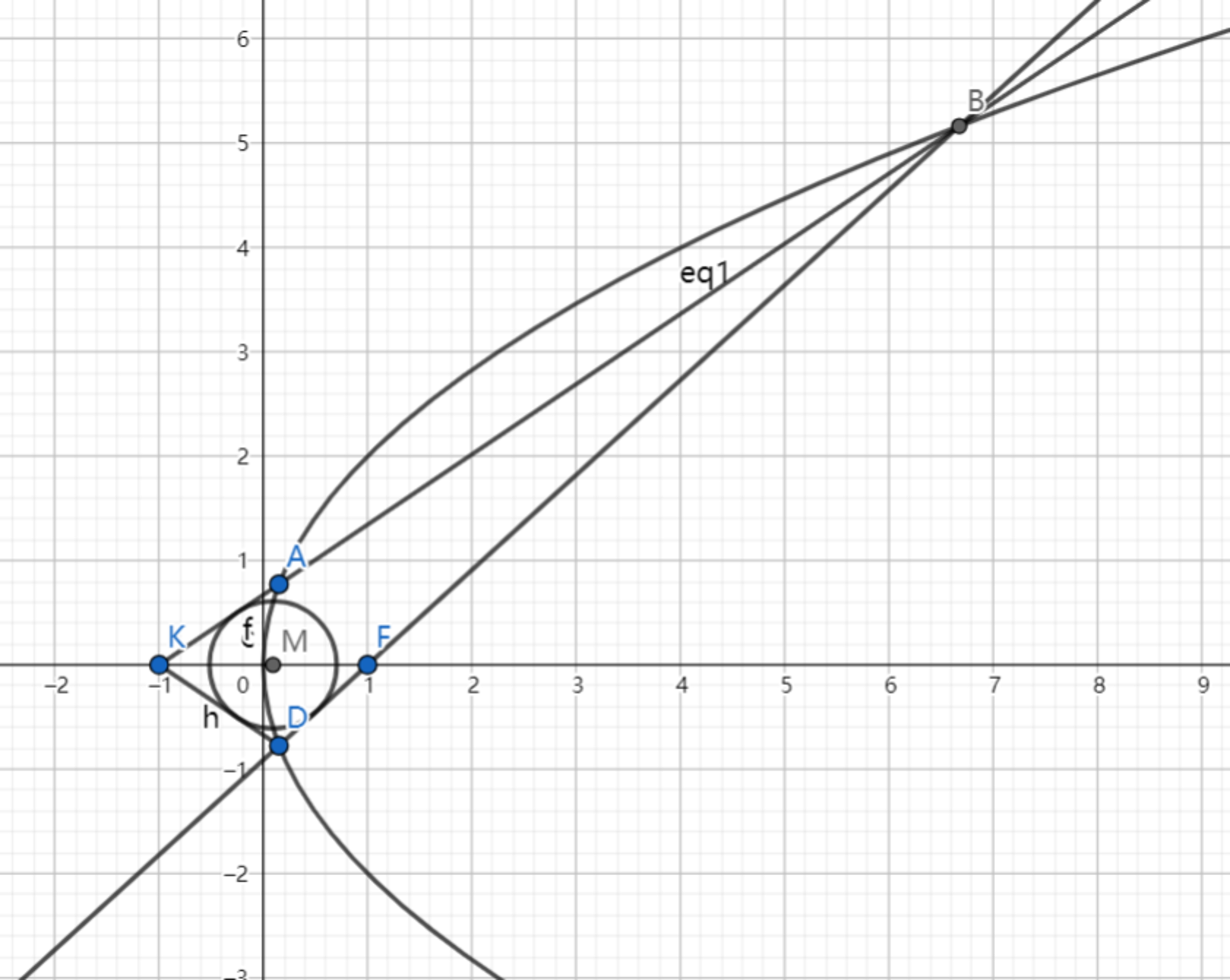
As shown above, point F is the focus of the parabola C : y 2 = 4 x , and line l passing through K ( − 1 , 0 ) intersects with C at point A , B , and A , D are symmetry about the x-axis.
If F A ⋅ F B = 9 8 , then find the equation of the incircle of △ B D K .
The equation can be expressed as: ( x − a ) 2 + ( y − b ) 2 = r 2 . Submit ⌊ 1 0 0 0 ( a + b + r ) ⌋ .
Have a look at my problem set: SAT 1000 problems
The answer is 777.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Centre of the circle is at ( 9 1 , 0 ) , and it's radius is 3 2 .
So the expression is equal to ⌊ 1 0 0 0 ( 9 1 + 0 + 3 2 ) ⌋ = 7 7 7 .
Let A have coordinates A ( 4 p 2 , p ) . Then the equation of line A K is y = p 2 + 4 4 p ( x + 1 ) , and the other intersection with parabola y 2 = 4 x is B ( p 2 4 , p 4 ) . As the focus of parabola y 2 = 4 x , F has coordinates F ( 1 , 0 ) , and by symmetry, D has coordinates D ( 4 p 2 , − p ) .
Since F A ⋅ F B = 9 8 , ( 4 p 2 − 1 ) ( p 2 4 − 1 ) = p ⋅ p 4 = 9 8 , which rearranges to 9 p 4 − 1 8 4 p 2 + 1 4 4 = 0 , or p = 3 1 ( ± 8 ± 2 7 ) . Without loss of generality, and to match the given picture, choose p = 3 1 ( 8 − 2 7 ) .
Substituting p = 3 1 ( 8 − 2 7 ) , the coordinates for B and D are now B ( 9 1 ( 2 3 + 8 7 ) , 3 2 ( 4 + 7 ) ) and D ( 9 1 ( 2 3 − 8 7 ) , 3 1 ( − 8 + 2 7 ) ) .
Using the distance formula, B D = 9 6 4 , B K = 9 1 0 2 3 + 8 7 , and D K = 9 1 0 2 3 − 8 7
The center ( a , b ) of the incircle of △ B D K is a = B D + B K + D K B D ⋅ K x + B K ⋅ D x + D K ⋅ B x and b = B D + B K + D K B D ⋅ K y + B K ⋅ D y + D K ⋅ B y , which solves to a = 9 1 and b = 0 .
The radius r of the incircle of △ B D K is r = s s ( s − B D ) ( s − B K ) ( s − D K ) where s = 2 1 ( B D + B K + D K ) , which solves to r = 3 2 .
Therefore, ⌊ 1 0 0 0 ( a + b + r ) ⌋ = 7 7 7 .