SAT1000 - P842
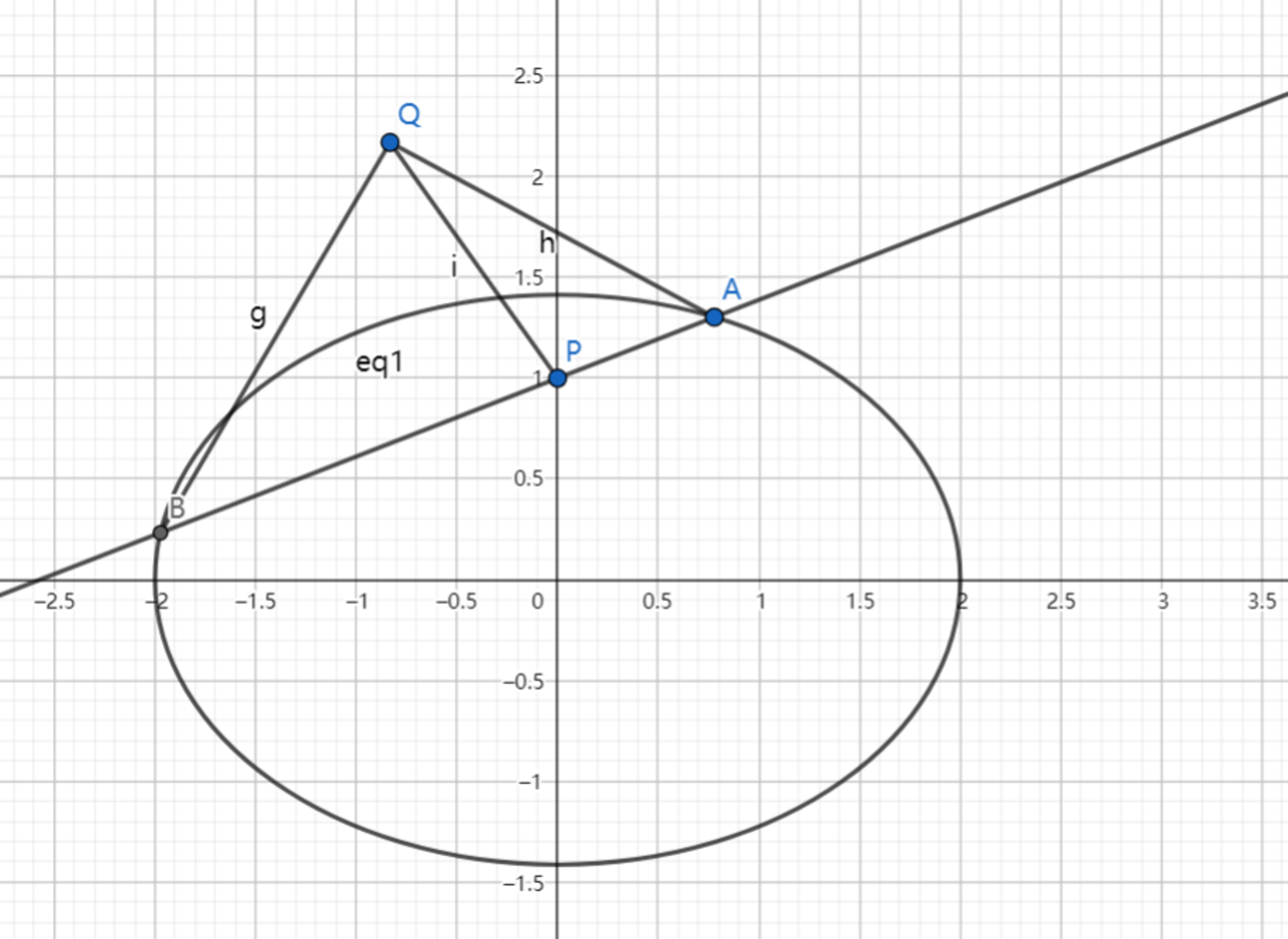
As shown above, the ellipse has equation: , and line passing through intersects with the ellipse at point .
Then there exists a fixed point so that the following equation always holds as rotates:
Then find the coordinate of .
The coordinate of is . Submit .
Have a look at my problem set: SAT 1000 problems
The answer is 4000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Since the equation always holds as l rotates, let's examine two convenient slopes for l , namely, m = 0 and m = 2 1 .
By the converse of the angle bisector theorem, the equation ∣ Q B ∣ ∣ Q A ∣ = ∣ P B ∣ ∣ P A ∣ means that ∠ P Q A = ∠ P Q B . Therefore, for m = 0 , where B , P , and A are evenly spaced out on a horizontal line with P on the y -axis, Q must also lie on the y -axis, so let the coordinates of Q be Q ( 0 , q ) .
Then for m = 2 1 , line l through P ( 0 , 1 ) would have an equation of y = 2 1 x + 1 , and would intersect the ellipse 4 x 2 + 2 y 2 = 1 at B ( − 2 , 0 ) and A ( 3 2 , 3 4 ) . Then by the distance formula, P B = 5 , P A = 3 5 , Q B = 4 + q 2 , Q A = 3 1 9 q 2 − 2 4 q + 2 0 , and substituting these into ∣ Q B ∣ ∣ Q A ∣ = ∣ P B ∣ ∣ P A ∣ and solving gives q 2 − 3 q + 2 = 0 which solves to q = 1 or q = 2 . It can't be q = 1 , because then P and Q would be the same point, so q = 2 , which means the coordinates of Q are ( 0 , 2 ) .
Therefore, x 0 = 0 , y 0 = 2 , and ⌊ 1 0 0 0 ( 2 y 0 − x 0 ) ⌋ = 4 0 0 0 .