SAT1000 - P845
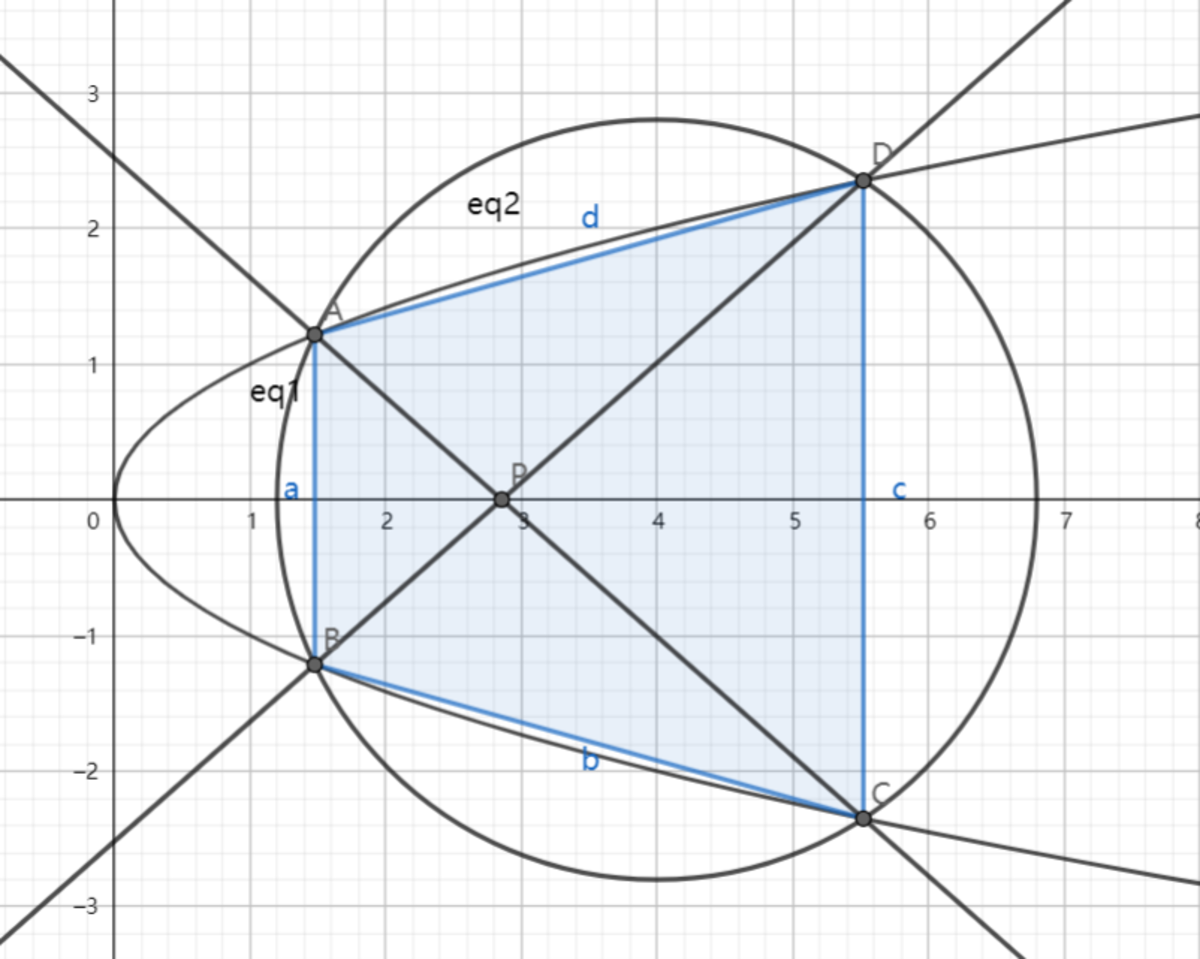
As shown above, the parabola and circle for intersect at points , , , and ; and their relative positions are shown in the figure. Lines and intersect at point .
Find the coordinates of as the area of quadrilateral reaches the maximum when varies. Submit .
Have a look at my problem set: SAT 1000 problems
The answer is 1166.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let us call the coordinates of A , B , C and D as ( x A , y A ) , ( x B , y B ) , ( x C , y C ) and ( x D , y D ) , respectively.
To find the y -values one just substitutes the parabola equation x = y 2 in the circle equation
( y 2 − 4 ) 2 + y 2 = r 2
y 4 − 7 y 2 + ( 1 6 − r 2 ) = 0
y 2 = 2 7 ± 4 r 2 − 1 5
So, since x = y 2 , we have:
( x A , y A ) = ⎝ ⎜ ⎛ 2 7 − 4 r 2 − 1 5 , 2 7 − 4 r 2 − 1 5 ⎠ ⎟ ⎞
( x B , y B ) = ⎝ ⎜ ⎛ 2 7 − 4 r 2 − 1 5 , − 2 7 − 4 r 2 − 1 5 ⎠ ⎟ ⎞
( x C , y C ) = ⎝ ⎜ ⎛ 2 7 + 4 r 2 − 1 5 , − 2 7 + 4 r 2 − 1 5 ⎠ ⎟ ⎞
( x D , y D ) = ⎝ ⎜ ⎛ 2 7 + 4 r 2 − 1 5 , 2 7 + 4 r 2 − 1 5 ⎠ ⎟ ⎞
The quadrilateral A B C D is actually a trapezoid, so its area (which I'll denote by S ) will be:
S = 2 1 [ ( y D − y C ) + ( y A − y B ) ] ⋅ ( x C − x A )
S = 2 1 ⎣ ⎢ ⎡ 2 2 7 + 4 r 2 − 1 5 + 2 2 7 − 4 r 2 − 1 5 ⎦ ⎥ ⎤ ⋅ 4 r 2 − 1 5
Since S is an area and, so, always a positive value, maximize S is the same as maximizing S 2 , which I'll call T :
T = S 2 = ( 4 r 2 − 1 5 ) ⋅ ( 7 + 6 4 − 4 r 2 )
Maximizing:
d r d T = 8 r ( 7 + 6 4 − 4 r 2 ) − ( 4 r 2 − 1 5 ) 2 6 4 − 4 r 2 8 r = 0
1 2 r 2 − 1 4 3 = 1 4 6 4 − 4 r 2
Squaring both sides:
1 4 4 r 4 + 7 8 4 r 2 + 7 9 0 5 = 0
r 2 = 3 6 5 2 7 or r 2 = 4 1 5
The condition r 2 = 4 1 5 will actually make S = 0 , so it's the minimizing condition. The maximizing condition is, then:
r 2 = 3 6 5 2 7
We will focus on points B and D , because P is the intersection of B D with the x -axis (the same could be made with the line A C ). So:
( x B , y B ) = ⎝ ⎜ ⎛ 6 2 1 − 1 4 2 , − 6 2 1 − 1 4 2 ⎠ ⎟ ⎞
( x D , y D ) = ⎝ ⎜ ⎛ 6 2 1 + 1 4 2 , 6 2 1 + 1 4 2 ⎠ ⎟ ⎞
The line B D has equation:
x = 3 1 4 y + 6 7
Just as a confirmation, points A and C have coordinates:
( x A , y A ) = ⎝ ⎜ ⎛ 6 2 1 − 1 4 2 , 6 2 1 − 1 4 2 ⎠ ⎟ ⎞
( x C , y C ) = ⎝ ⎜ ⎛ 6 2 1 + 1 4 2 , − 6 2 1 + 1 4 2 ⎠ ⎟ ⎞
And the line A C has equation:
x = − 3 1 4 y + 6 7
So:
x 0 = 6 7 → ⌊ 1 0 0 0 x 0 ⌋ = 1 1 6 6