SAT1000 - P846

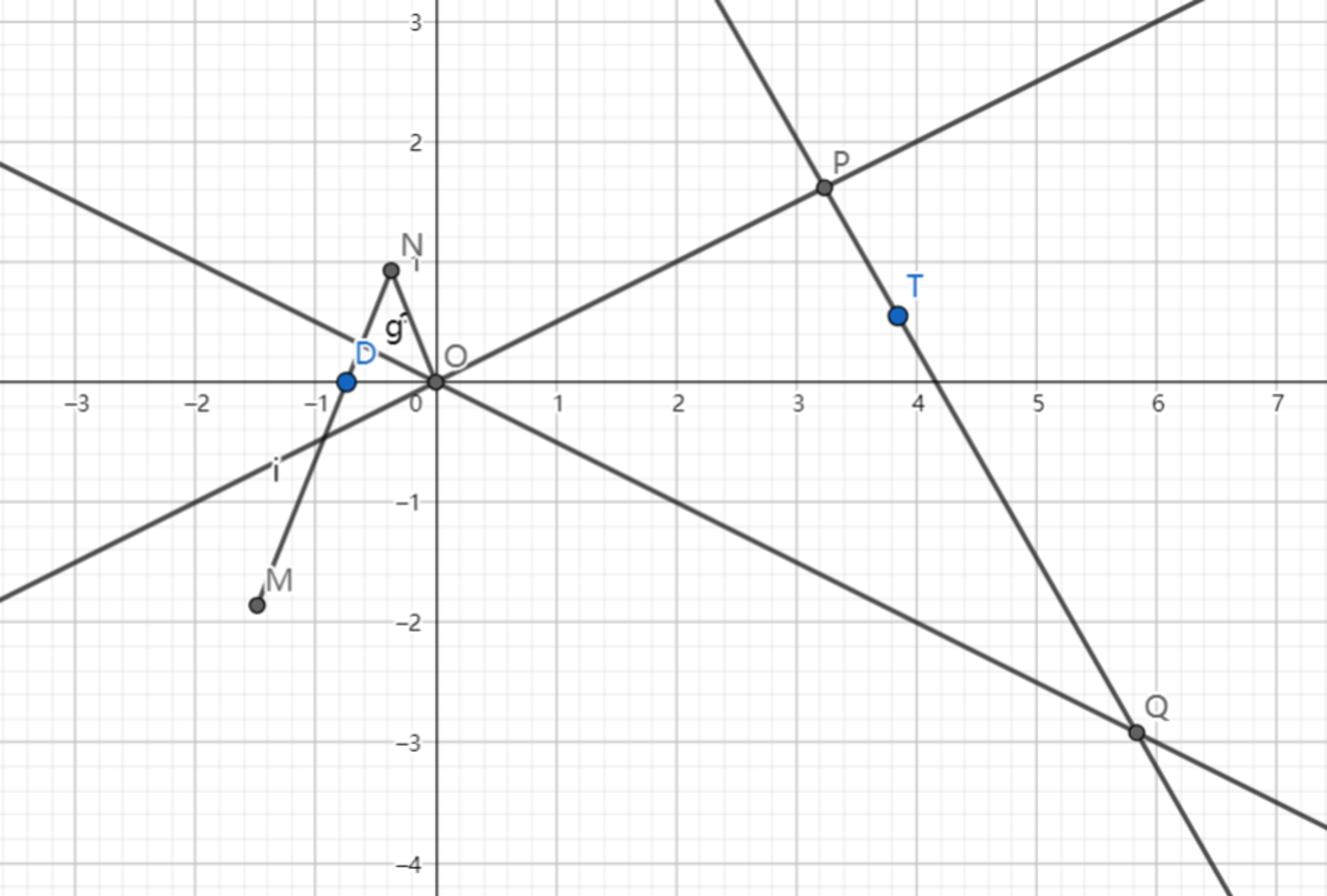
As shown above, $ON, NM$ are rigid rods and $DN=ON=1,MN=3$ , $O(0,0)$ is fixed on the coordinate plane, and $D$ is restricted along the x-axis. Then as $D$ moves horizontally, point $M$ will rotate around point $O$ . Curve $C$ is the locus of point $M$ .

If line $l$ intersects with $l_1:x-2y=0$ at point $P$ , $l_2:x+2y=0$ at point $Q$ , and $l$ is tangent to curve $C$ .

Then find the minimum area of $\triangle OPQ$ when line $l$ moves and rotates.

Let $S$ be the minimum area. Submit $\lfloor 1000S \rfloor$ .

---

Have a look at my problem set: SAT 1000 problems