SAT1000 - P886

Geometry Level pending

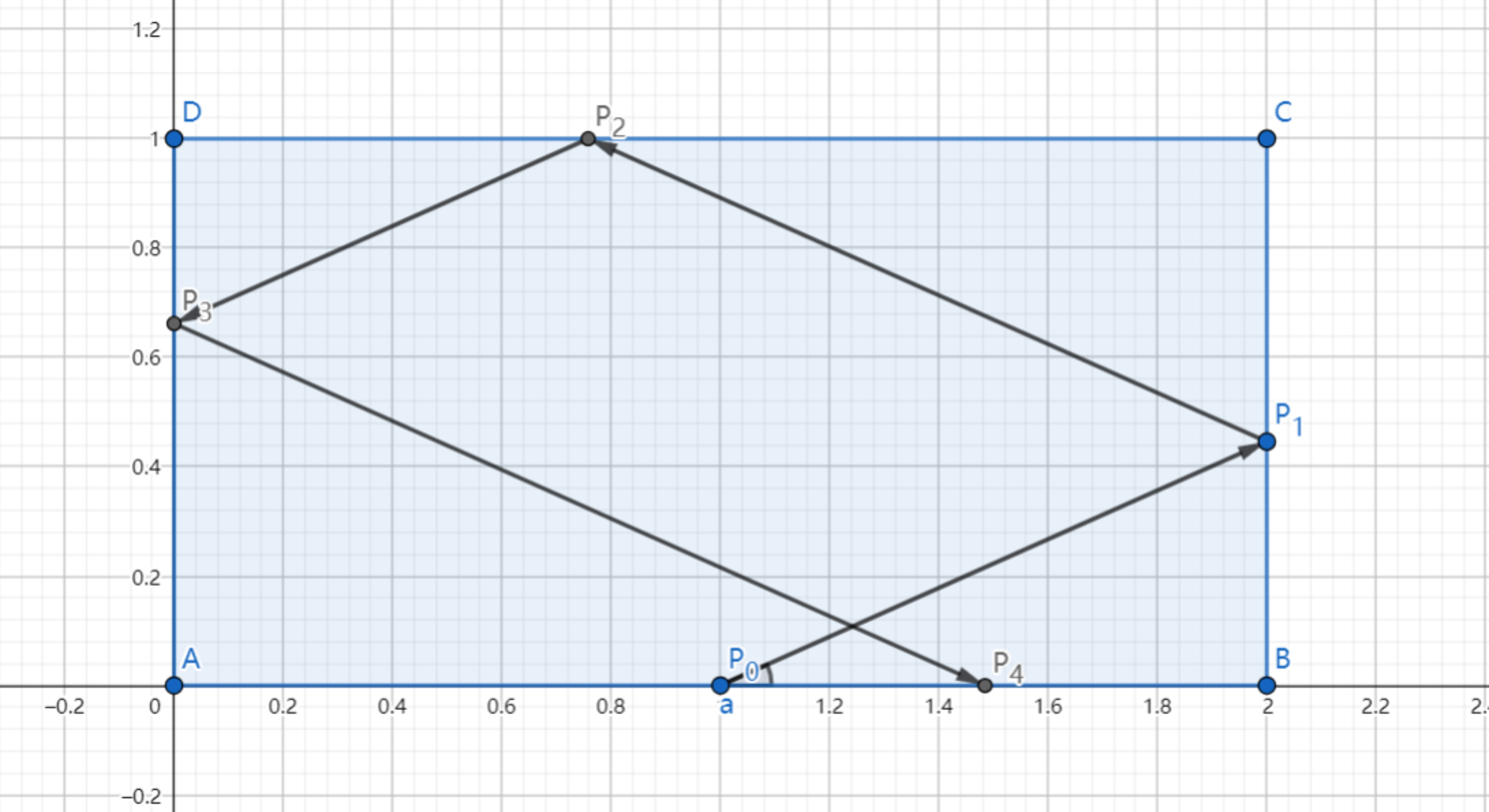
As shown above, the four vertices of the mirror rectangle are $A(0,0), B(2,0), C(2,1), D(0,1)$ . A ray is emitted from $P_0(1,0)$ at angle $\theta$ with $AB$ and reflected at $P_1$ on $BC$ , $P_2$ on $CD$ , $P_3$ on $DA$ , $P_4$ on $AB$ following the law of reflection. If $P_4$ has coordinate $(x_4,0)$ and $x_4 \in (1,2)$ , find the range of $\tan \theta$ . Let the range be $(l,r)$ . Submit $\lfloor 1000(2r-l) \rfloor$ .

Have a look at my problem set: SAT 1000 problems

The answer is 600.

2 solutions

David Vreken
Jun 27, 2020

Extend reflections of the mirror rectangle so that the path of the ray is represented as a straight line:

Then by the given limitations, the ray can go between $Q(5, 2)$ and $R(6, 2)$ , for a range of $\tan \theta$ of $(\frac{2}{5}, \frac{1}{2}$ ), so $l = \frac{2}{5}$ , $r = \frac{1}{2}$ , and $\lfloor 1000(2r - l) \rfloor = \boxed{600}$ .

A Former Brilliant Member
Jun 27, 2020

Position coordinates of $P_1$ are $(2,\tan \theta)$ , of $P_2$ are $(3-\cot \theta, 1)$ , of $P_3$ are $(0,2-3\tan \theta)$ and of $P_4$ are $(2\cot \theta -3,0)$ .

So, $1<2\cot \theta-3<2\implies 0.4<\tan \theta <0.5$ , and the required answer is $\boxed {600}$ .

SAT1000 - P886

The answer is 600.

2 solutions

0 pending reports