SAT1000 - P887
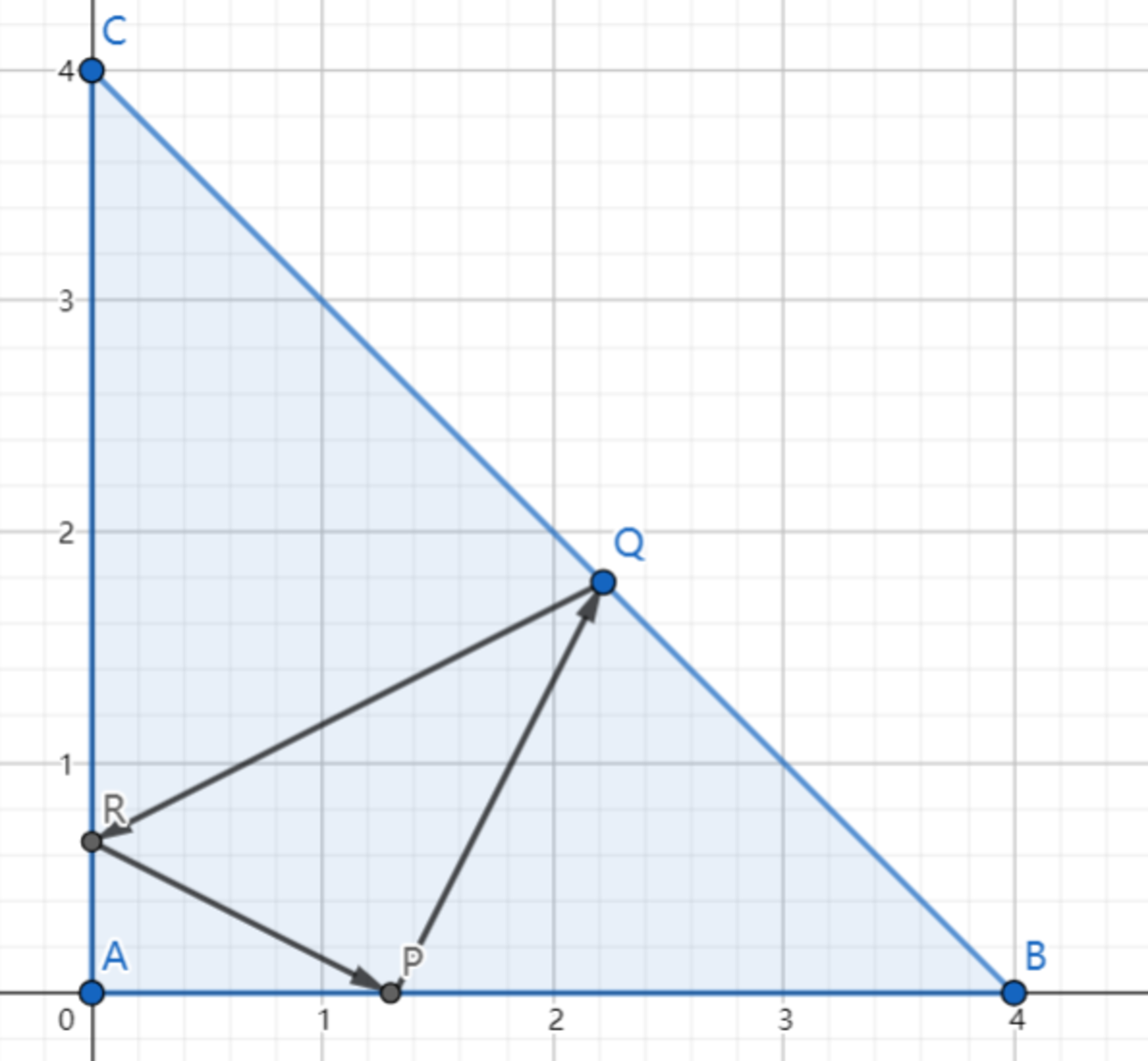
As shown above, in △ A B C , A = 9 0 ° , A B = A C = 4 , and P is a point on segment A B (excluding points A and B ). A ray is emitted from P and it is reflected at Q on B C , R on A C and returned to point P again. If ray Q R passes through the centroid of △ A B C , find the length of A P .
Submit ⌊ 1 0 0 0 ∣ A P ∣ ⌋ .
Have a look at my problem set: SAT 1000 problems
The answer is 1333.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
△ P Q R is a right-angled triangle with right angle at P . Let ∠ A P R = α , position coordinates of Q be ( h , k ) , and ∣ A P ∣ = a .
Then, k = ( h + a ) tan α , h = a + k tan α ⟹
h = a sec 2 α , k = a tan 2 α
⟹ a ( sec 2 α + tan 2 α ) = 4
⟹ a = 1 + sin 2 α 4 cos 2 α
Centeroid of the triangle is at ( 3 4 , 3 4 )
Therefore 3 4 = ( 3 4 + a ) tan α
⟹ 2 tan 3 α − 5 tan 2 α + 4 tan α − 1 = 0
⟹ tan α = 1 , 2 1
For tan α = 1 ( α = 4 5 ° ) , the ray from P will be incident normally to the surface B C , and is so discarded.
For tan α = 0 . 5 , a = 3 4 ≈ 1 . 3 3 3 3 3 3 , and the required answer is 1 3 3 3 .
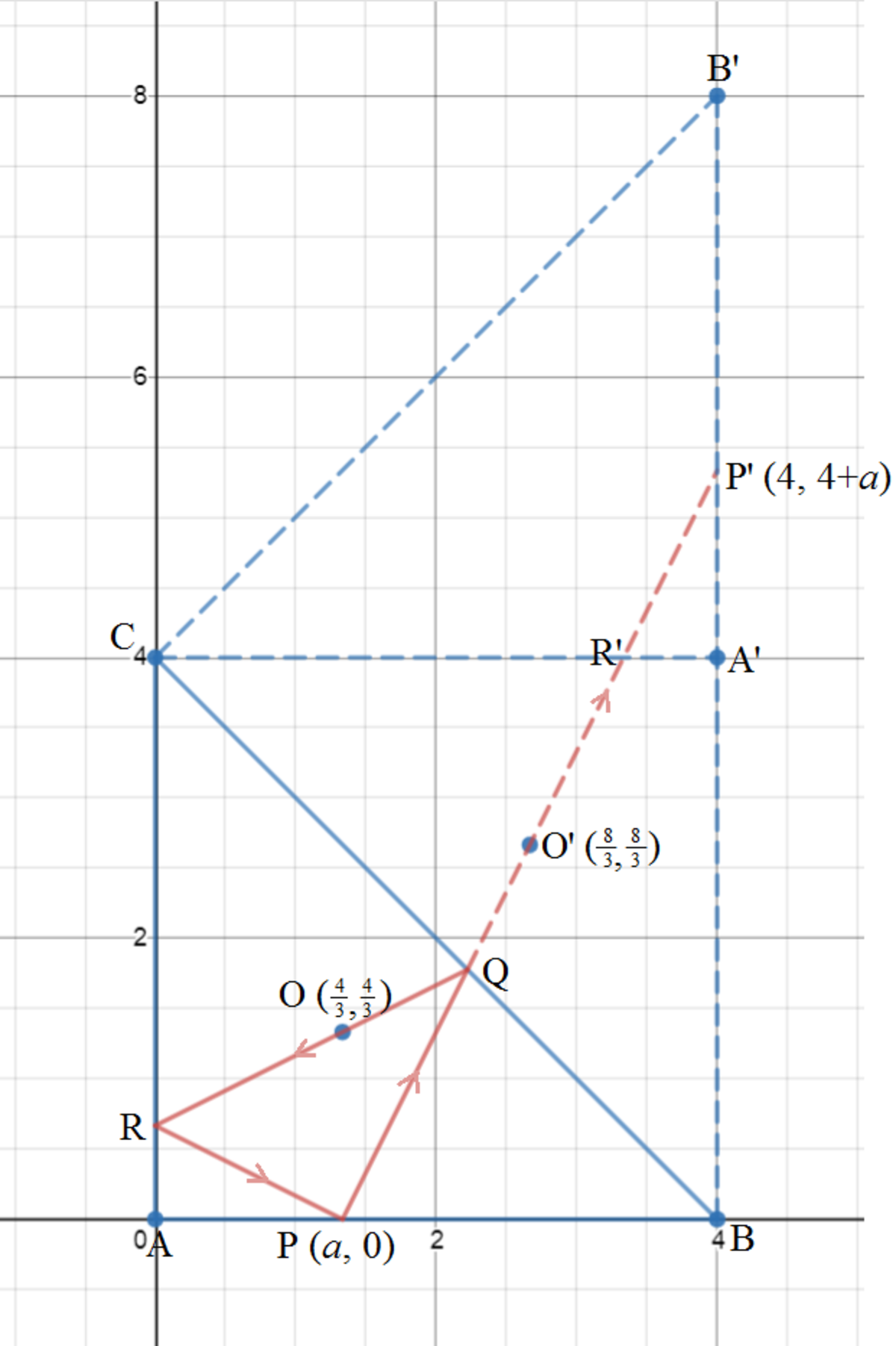
Extend the reflected beam with dashed line behind the mirror and the respective image points be label with a prime. Let A P = a ; then P ( a , 0 ) and its image P ′ ( 4 , 4 + a . Note the centroid O ( 3 4 , 3 4 ) and its image O ′ ( 3 8 , 3 8 ) .
Then the line P P ′ is given by:
x − 3 8 y − 3 8 ⟹ y = B P B P ′ = 4 − a 4 + a = 4 − a 4 + a ( x − 3 8 ) + 3 8
Since at P ( a , 0 ) , y = 0 when x = a , we have:
4 − a 4 + a ( a − 3 8 ) + 3 8 ( 4 + a ) ( a − 3 8 ) + 3 8 ( 4 − a ) 4 a + a 2 − 3 1 6 a ⟹ a = 0 = 0 = 0 = 3 1 6 − 4 = 3 4
Therefore, ⌊ 1 0 0 0 a ⌋ = 1 3 3 3 .
Extend the reflections of the triangle mirror so that the path of the ray is represented as a straight line, and label the diagram as follows, including M (the midpoint of A and B ) and N (the centroid of △ A ′ B C ):
Since the centroid is located 3 2 of the distance from a vertex to its opposite midpoint, A ′ M A ′ N = 3 2 . Since △ A ′ M S ∼ A ′ N T by AA similarity, A ′ S A ′ T = A ′ M A ′ N or 2 A ′ T = 3 2 , which solves to A ′ T = 3 4 . That means the x -coordinate of N is A B − A ′ T = 4 − 3 4 = 3 8 . By similarity, the y -coordinate of N is also 3 8 , so the coordinates of N are N ( 3 8 , 3 8 ) .
Let k = A P = A ′ P " . Then the coordinates of P are P ( k , 0 ) and the coordinates of P ′ are P ′ ( 4 , k + 4 ) , and the equation of the line through P and P ′ is y = − k − 4 k + 4 ( x − k ) .
N ( 3 8 , 3 8 ) is on y = − k − 4 k + 4 ( x − k ) , so 3 8 = − k − 4 k + 4 ( 3 8 − k ) , which solves to k = 3 4 .
Therefore, ∣ A P ∣ = k = 3 4 and ⌊ 1 0 0 0 ∣ A P ∣ ⌋ = 1 3 3 3 .