SAT1000 - P888
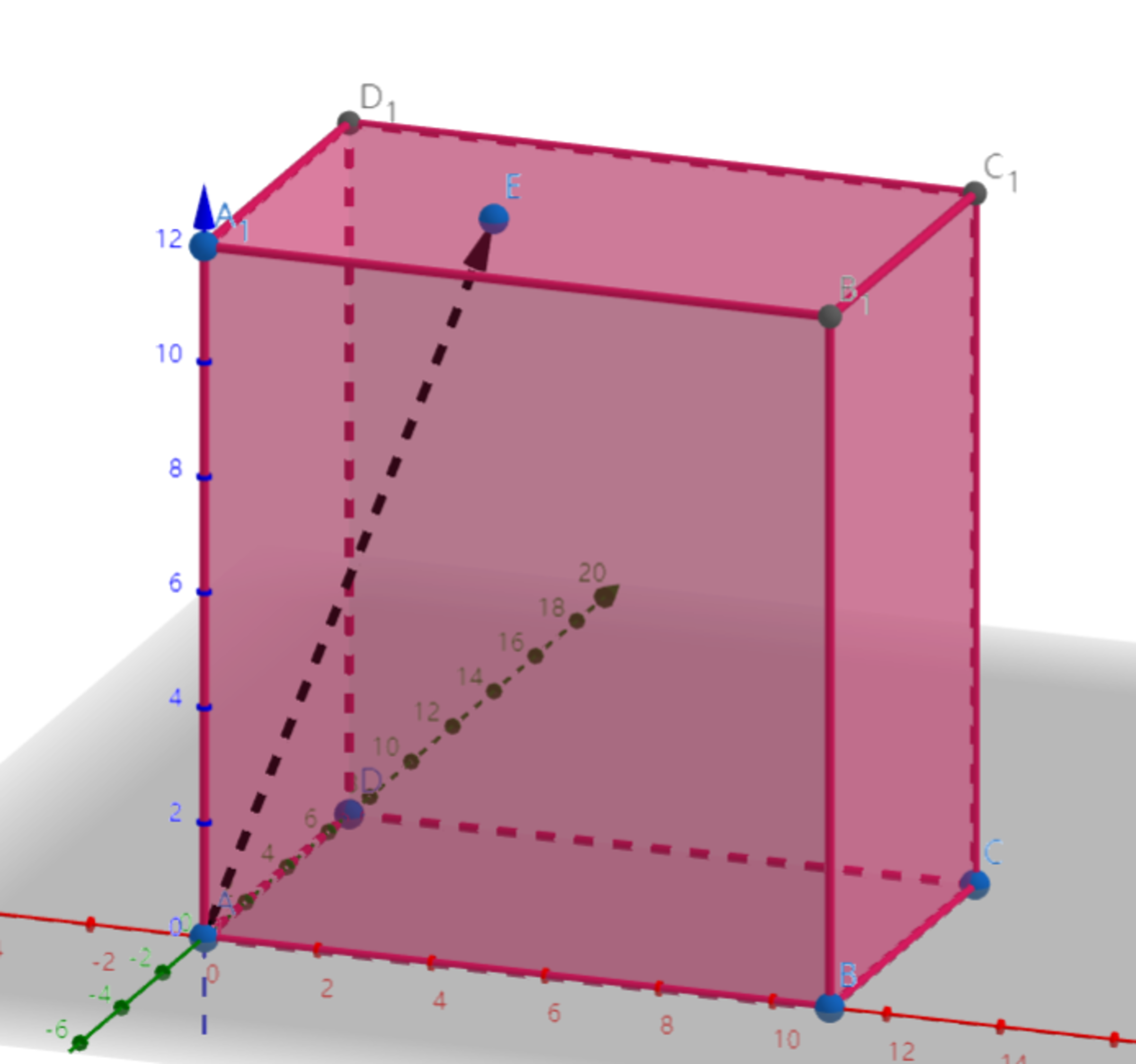
As shown above, in cuboid A B C D − A 1 B 1 C 1 D 1 , A B = 1 1 , A D = 7 , A A 1 = 1 2 . The faces of the cuboid are all mirrors.
A ray is emitted from A ( 0 , 0 , 0 ) to E ( 4 , 3 , 1 2 ) and reflected when meeting the faces of the cuboid following the reflection law. Let L i denote the length of the ray between the ( i − 1 ) t h reflection to the i t h reflection ( i = 2 , 3 , 4 ) , L 1 = A E .
Compare L 1 , L 2 , L 3 , L 4 .
A . L 1 = L 2 > L 3 = L 4
B . L 1 = L 2 = L 3 = L 4
C . L 1 = L 2 > L 3 < L 4
D . L 1 = L 2 > L 3 > L 4
Have a look at my problem set: SAT 1000 problems
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Extend reflections of the mirror cuboid so that the path of the ray is represented as a straight line. Since the ray goes through ( 0 , 0 , 0 ) and ( 4 , 3 , 1 2 ) , it has parametric equations x = 4 t , y = 3 t , and z = 1 2 t and will intersect a mirror plane of one of the reflected cuboids at x = 1 1 n , y = 7 n , and z = 1 2 n for integers n ≥ 0 .
Combining equations above gives t = 4 1 1 n , t = 3 7 n , and t = n , and testing the first few integer values of n and sorting by t give I n = ( t , x , y , z ) values of I 0 = ( 0 , 0 , 0 , 0 ) , I 1 = ( 1 , 4 , 3 , 1 2 ) , I 2 = ( 2 , 8 , 6 , 2 4 ) , I 3 = ( 3 7 , 3 2 8 , 7 , 2 8 ) , and I 4 = ( 4 1 1 , 1 1 , 4 3 3 , 3 3 ) .
Using the distance equation on the values above, L 1 = 1 3 , L 2 = 1 3 , L 3 = 3 1 3 , and L 4 = 1 2 6 5 , so L 1 = L 2 > L 3 < L 4 , which is choice C .