SAT1000 - P894
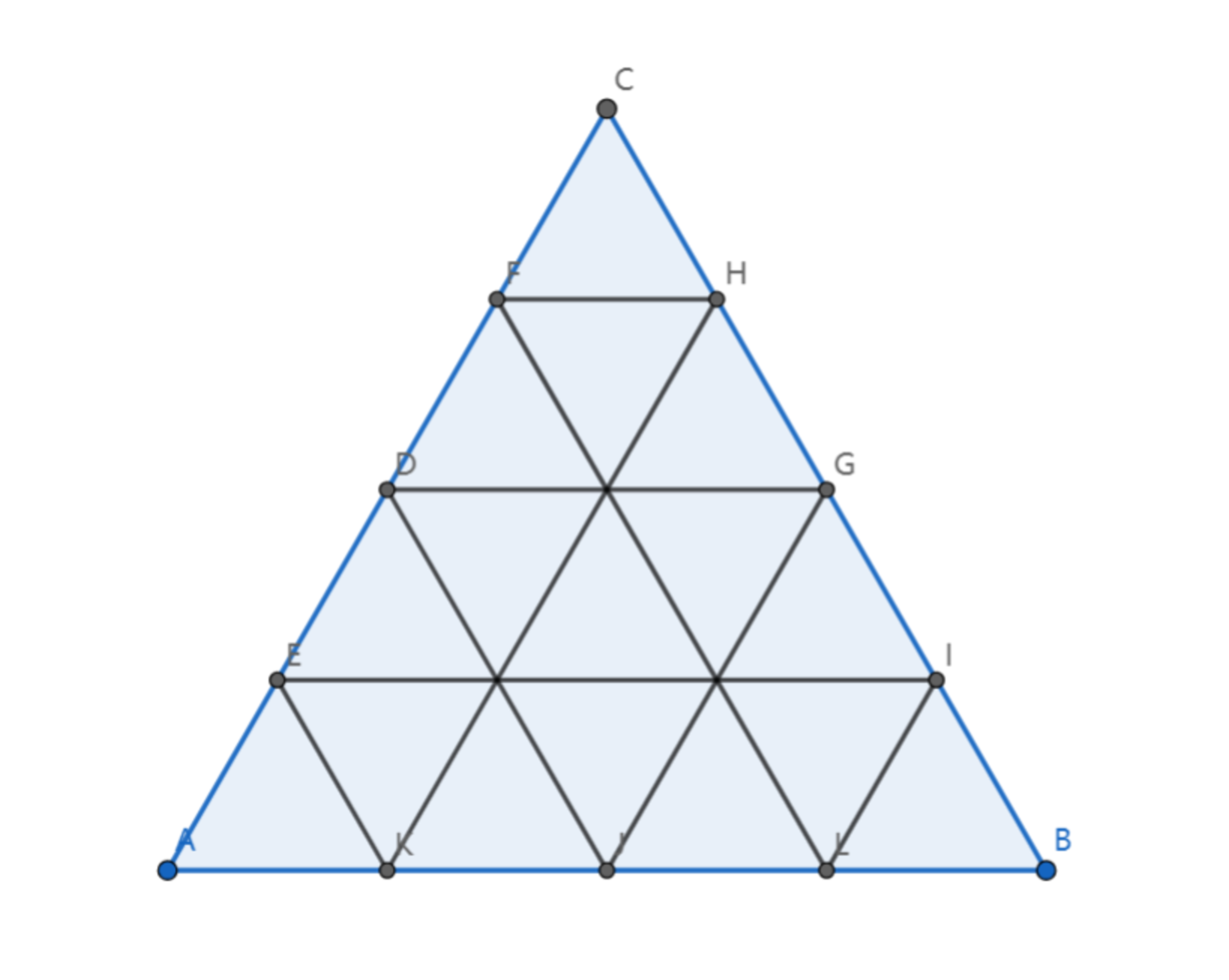
Imagine an equilateral △ A B C divided into n 2 ( n ≥ 2 , n ∈ N + ) congruent equilateral pieces. (The image above shows n = 4 case).
Let's put each number on every vertex of all triangles, so that the numbers on the same side of △ A B C or on the same line parallel to the sides of △ A B C (if there’re exactly or more than 3 numbers) form arithmetic progressions .
a , b , c denote the number on vertices A , B , C respectively, a , b , c are not equal to each other and a + b + c = 1 .
Let f ( n ) denote the sum of all numbers on the vertices, find f ( 2 0 2 0 ) .
Have a look at my problem set: SAT 1000 problems
The answer is 681077.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
All the vertices is some linear combination of a , b , c (i.e. the number on vertex V can be expressed as p v a + q v b + r v c , where p v , q v , r v are some constants.)
However, a , b , c is symmetric in the sum, so the sum is definitely in the form of k a + k b + k c , where k is a constant, so we only need to find k . This means for every a , b , c satisfying a + b + c = 1 , f ( 2 0 2 0 ) doesn't vary with the choose of a , b , c .
Hence assume that every number on the vertices is 3 1 and you will ge the answer.
Let A be the top vertex of the equilateral triangle, B be the bottom left, and C , bottom right. Let the common difference of the arithmetic progression be d and put the values on the vertices as shown. Row 1 ( A being on the row 0 ) starts with a + d and ends with a + 2 d . Row 2 starts with a + 2 d and ends with a + 4 d , Row 3 starts with a + 3 d and ends with a + 6 d , and so on. We note that row k starts with a + k d and ends with a + 2 k d . We also note that, for an n -row equilateral triangle, b = a + n d and c = b + n d = a + 2 n d . Therefore, a + b + c = 3 a + 3 n d = 1 ⟹ a + n d = 3 1 .
For an n -row case, there is a total of T n a , where T n + 1 is the n th triangular number. On the k th row there are k + 1 vertices and the number of d starts with k d and ends with 2 k d . The sum of all the vertex numbers is given by:
f ( n ) = T n + 1 a + k = 1 ∑ n 2 ( k + 1 ) ( k + 2 k ) d = 2 ( n + 1 ) ( n + 2 ) + 2 3 d k = 1 ∑ n k ( k + 1 ) = 2 ( n + 1 ) ( n + 2 ) + 2 3 d k = 1 ∑ n ( k 2 + k ) = 2 ( n + 1 ) ( n + 2 ) + 2 3 d ( 6 n ( n + 1 ) ( 2 n + 1 ) + 2 n ( n + 1 ) ) = 2 ( n + 1 ) ( n + 2 ) + 4 d n ( n + 1 ) ( 2 n + 1 + 3 ) = 2 ( n + 1 ) ( n + 2 ) + 2 n ( n + 1 ) ( n + 2 ) d = 2 ( n + 1 ) ( n + 2 ) ( a + n d ) = 6 ( n + 1 ) ( n + 2 ) Note that a + n d = 3 1
Therefore, f ( 2 0 2 0 ) = 6 2 0 2 1 × 2 0 2 2 = 6 8 1 0 7 7 .