SAT1000 - P907
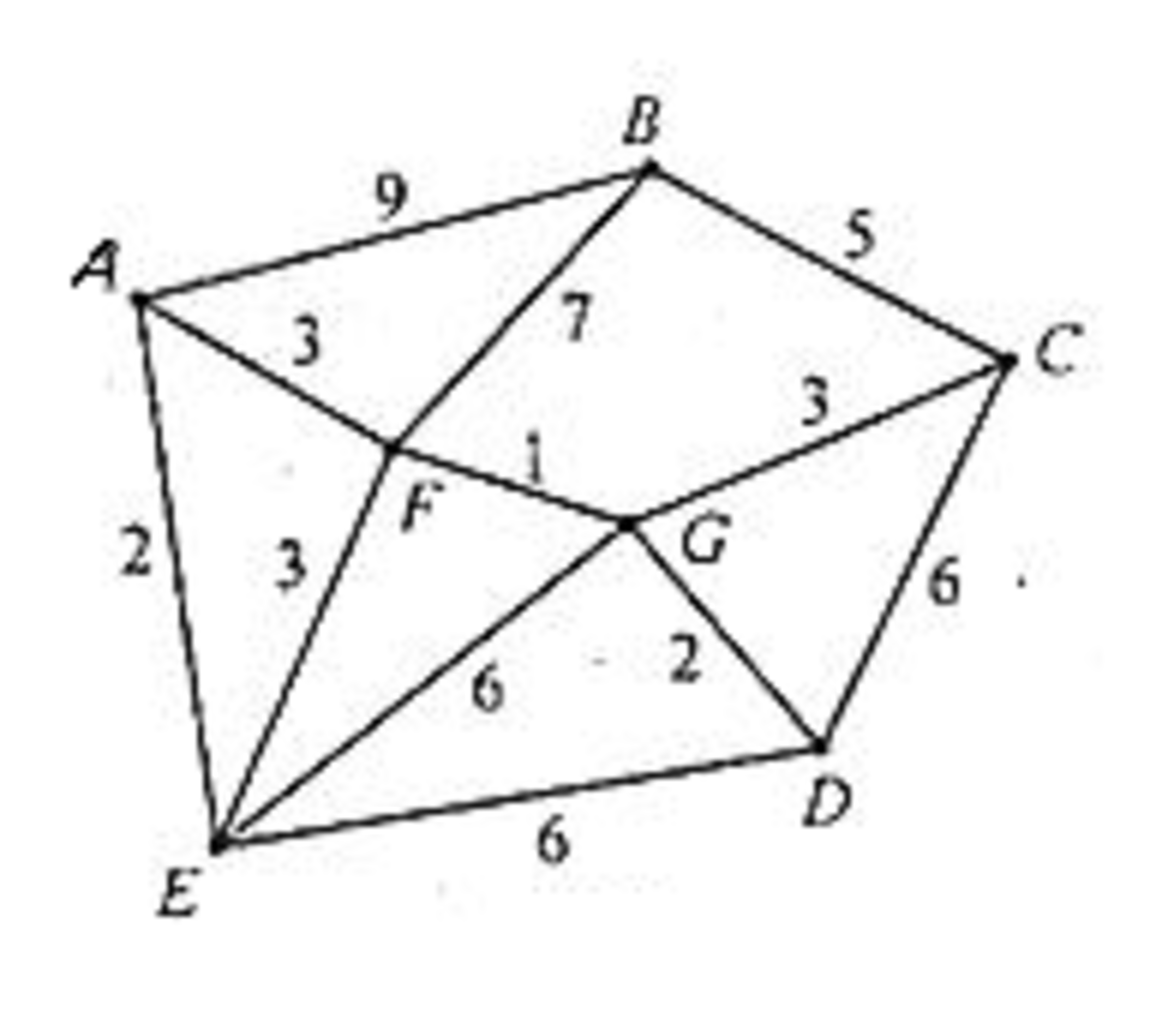
The image shows all of the available roads for road construction, where the letters represent cities and the numbers denote the corresponding cost for certain road.
What's the minimum total cost to construct roads so that one can travel from any city to every other one?
Have a look at my problem set: SAT 1000 problems
The answer is 16.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Going through each city, choosing the least costly road for each one, and connecting the grid will get you this result:
Counting the prices will give you a total cost of 1 6 units of currency.