SAT1000 - P929

All the $S_i^{'s}$ will be positive except for $i=13,14,27,28,41,42,55,56,69,70,83,84,97,98$ where the values go zero. Hence the required answer is $100-14=\boxed {86}$ .

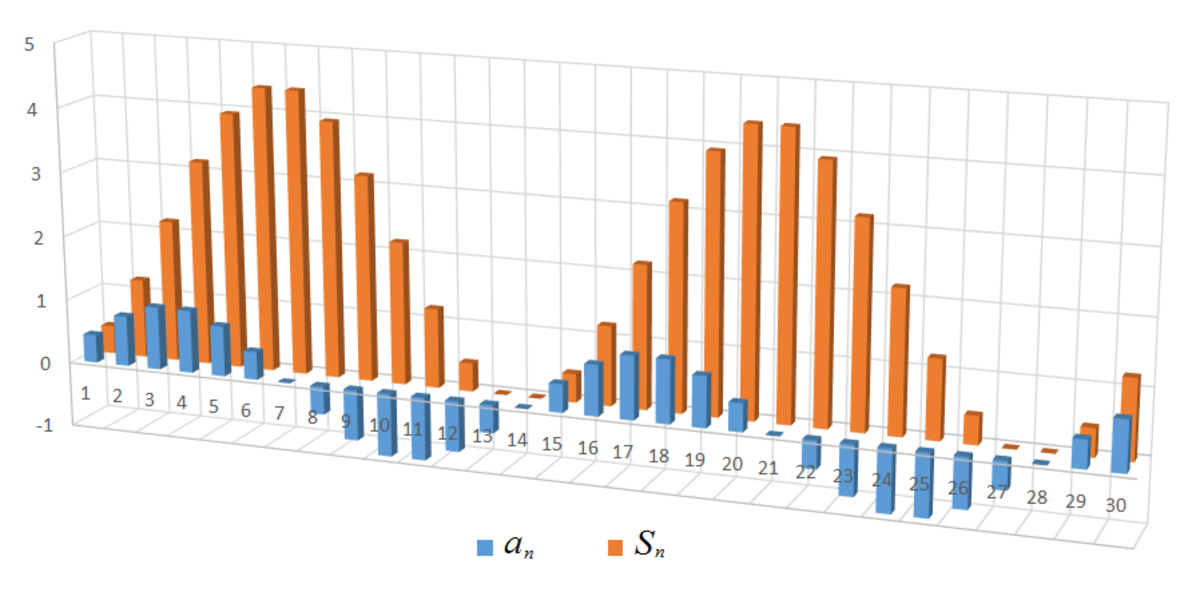
We note that $a_n = \sin \frac {n\pi}7$ is periodic with a period of $14$ ; $a_{n+7} = - a_n$ and $a_{7n} = 0$ , where $n$ is a positive integer. Therefore $S_n = \sum_{k=1}^n a_k$ is also periodic with a period of $14$ , $S_n = S_{13-n}$ and $S_{14n}=0$ . Let $S_0 = \sin 0 = 0$ , which does not affect $S_n$ for $n > 0$ . Then $S_{13} = S_{13-13} = S_0 = 0$ . There are $S_{13} = S_{14} = 0$ within a period and the rest of $S_1, S_2, S_3, \cdots S_{12} > 0$ . Therefore there are $100 - 2 \times \left \lfloor \frac {100}{14} \right \rfloor = \boxed{86}$ positive numbers fpr $S_1, S_2, S_3, \cdots S_{100}$ .