SAT1000 - P931
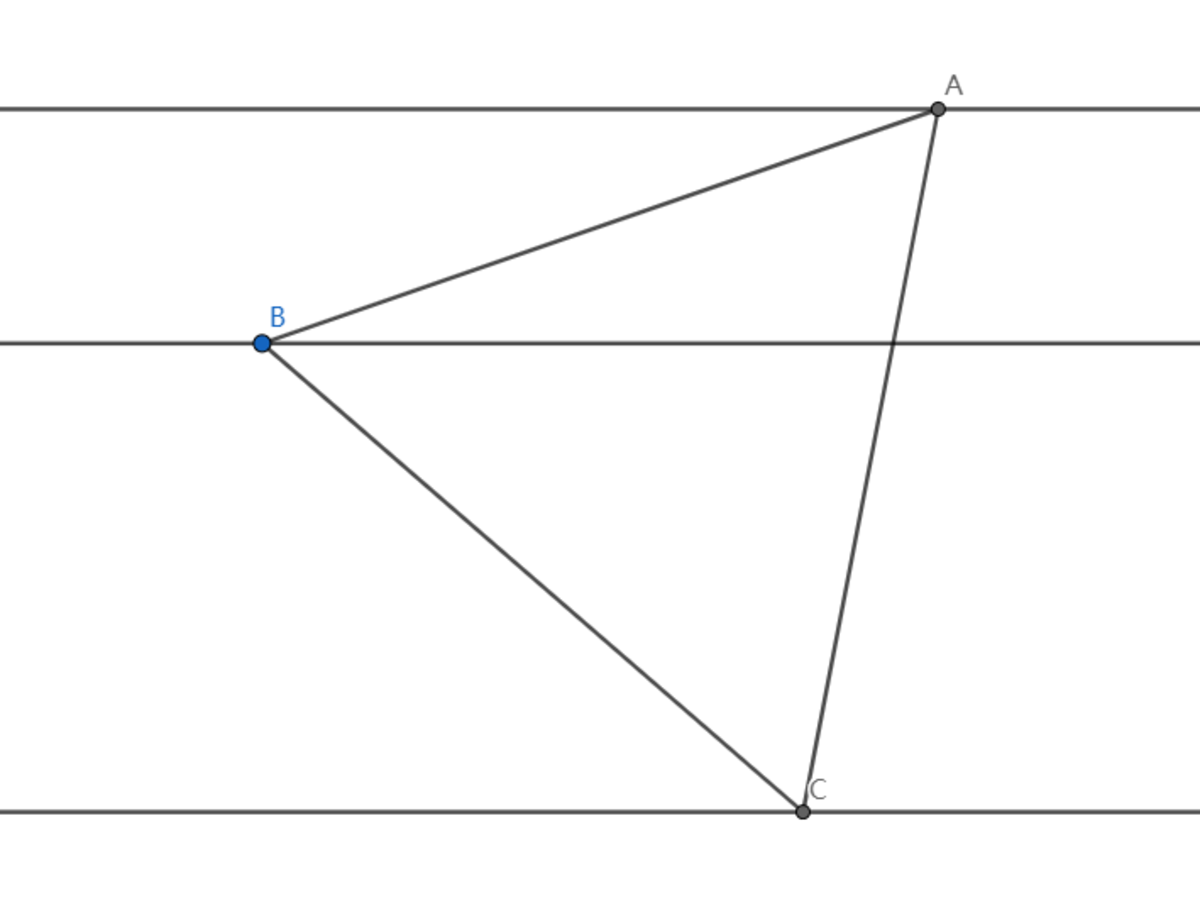
As shown above, from top to bottom, l 1 , l 2 , and l 3 are three parallel lines on the same plane, and the distance from l 1 to l 2 is 1 , the distance from l 2 to l 3 is 2 , and point A , B , C are on l 1 , l 2 , l 3 respectively.
If △ A B C is an equilateral triangle , then find the side length of △ A B C .
Let l denote the side length. Submit ⌊ 1 0 0 0 l ⌋ .
Have a look at my problem set: SAT 1000 problems
The answer is 3055.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Place the figure onto the xy-plane. Let the difference between the x-coordinates of A and B be a and let the difference between the x-coordinates of B and C be b . It follows that a 2 + 1 = l 2 , b 2 + 4 = l 2 , and ( a − b ) 2 + 9 = l 2 .
Using the first two equations, we conclude that a 2 = b 2 + 3 . Substituting this into the third equation and expanding yields 2 b 2 − 2 b b 2 + 3 + 1 2 = b 2 + 4 which is equivalent to 3 b 4 − 4 b 2 − 6 4 = 0 for positive b . Applying the quadratic formula and solving for b yields b = 3 4 3 . Substituting this value for b into b 2 + 4 = l 2 gives us l = 3 2 8 . ⌊ 1 0 0 0 l ⌋ = 3 0 5 5 .
Let the measure of the angle between A B and line l 2 be θ . Then we have:
⎩ ⎪ ⎨ ⎪ ⎧ sin θ = l 1 sin ( 6 0 ∘ − θ ) = l 2 . . . ( 1 ) . . . ( 2 )
From ( 2 ) :
2 3 cos θ − 2 1 sin θ 2 3 cos θ tan θ ⟹ sin θ ( 1 ) : ⟹ l ⟹ ⌊ 1 0 0 0 l ⌋ = l 2 = 2 sin θ = 2 5 sin θ = 5 3 = 5 2 + 3 3 = 2 8 3 = sin θ 1 = 3 2 8 ≈ 3 . 0 5 5 0 5 0 4 6 3 = 3 0 5 5 As ( 1 ) : sin θ = a 1