SAT1000 - P933

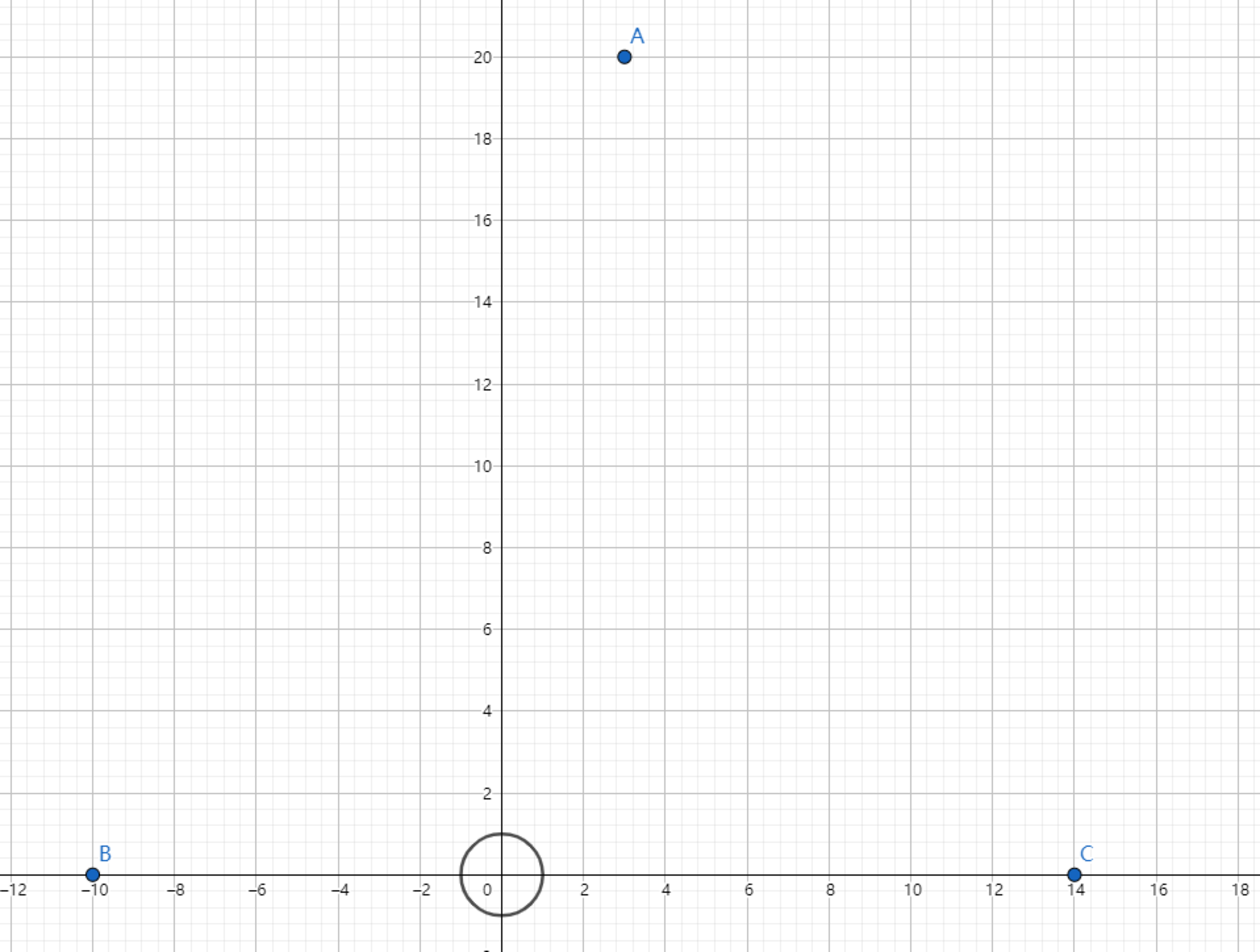
In the rectangular coordinate plane, the Taxicab path from point $M$ and $N$ is such path that moves only horizontally or vertically from $M$ to $N$ . And $d(M,N)$ denotes the length of the path.

Given that $A_1(3,20), A_2(-10,0), A_3(14,0)$ , we want to find a point $P(x_0,y_0)\ (y_0 \geq 0)$ so that $\displaystyle \sum_{k=1}^{3} d(P,A_k)$ has the minimum value.

However, the Taxicab path from $P$ to each point can't pass through the region: $x^2+y^2<1$ .

Then find the coordinates of $P$ .

If $P$ has coordinate $(x_0,y_0)$ , submit $2y_0-x_0$ .

---

Have a look at my problem set: SAT 1000 problems