SAT1000 - P939

Geometry Level 5

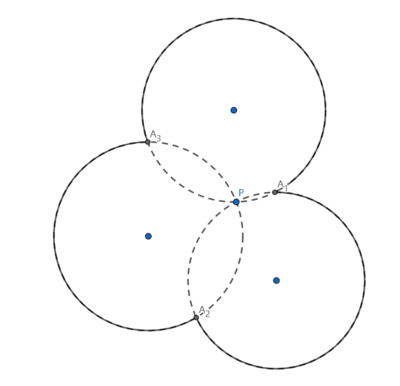
As shown above, the enclosed curve $C$ is composed of three segments of arcs (solid line) and the circles that the arcs belong to pass through the same point $P$ , and they have the same radius. If the $k$ th segment of arc corresponds the center angle $\alpha_k$ , where $k=1,2,3$ , find the value of:

$\cos \dfrac{\alpha_1}{3} \cos \dfrac{\alpha_2+\alpha_3}{3} - \sin \dfrac{\alpha_1}{3} \sin \dfrac{\alpha_2+\alpha_3}{3}$

Let $A$ denote the value. Submit $\lfloor 1000A \rfloor$ .

Have a look at my problem set: SAT 1000 problems

The answer is -500.

1 solution

David Vreken
Jul 16, 2020

Label the angles in the diagram as follows:

By the inscribed angle theorem, $\alpha_1 = 2\beta_1$ , $\alpha_2 = 2\beta_2$ , and $\alpha_3 = 2\beta_3$ . Also, $\beta_1 + \beta_2 + \beta_3 = 360°$ .

Using the cosine of a sum equation and then substituting the values above,

$A = \cos (\frac{\alpha_1}{3}) \cos (\frac{\alpha_2 + \alpha_3}{3}) - \sin (\frac{\alpha_1}{3}) \sin (\frac{\alpha_2 + \alpha_3}{3})$

$A = \cos (\frac{\alpha_1}{3} + \frac{\alpha_2 + \alpha_3}{3})$

$A = \cos (\frac{1}{3}(\alpha_1 + \alpha_2 + \alpha_3))$

$A = \cos (\frac{1}{3}(2\beta_1 + 2\beta_2 + 2\beta_3))$

$A = \cos (\frac{2}{3}(\beta_1 + \beta_2 + \beta_3))$

$A = \cos (\frac{2}{3} \cdot 360°)$

$A = \cos (240°)$

$A = -\frac{1}{2}$

Therefore, $\lfloor 1000A \rfloor = \boxed{-500}$ .

SAT1000 - P939

The answer is -500.

1 solution

0 pending reports